Introduction

The functions described next cover the art of combining two (or more) tables using the fine arts of relational algebra where different algebraic rules can be applied to rows and columns.

In a simple example, two tables with members of two clubs (e.g. tennis and squash) need to be merged into one where the last and first names of the members shall act as matching identifiers. In case no person has a membership in both clubs, no overlap applies, and the list will simply be appended where the data are aligned to the right columns, using header names as orientation. The columns in both tables do not need to be aligned before the merger. If one or more persons possess memberships in both clubs, then the information will be consolidated where the same consolidation actions rules are available as used by table consolidate. As an example, the account receivable (e.g. indoor court reservation fees to be balanced) can be added up whereas the preferences at the club bar can be consolidated with append once so the preference for tonic water at one club and beer at the other club will appended into "tonic water, beer".

If no identifier columns are defined in the functions described next, then every row will be considered unique. Merging the table is treated appending two tables, with aligning the data into the right columns.

The following table summarizes the 25 functions in a 5 x 5 matrix with specifc rules to be applied on rows as wll as columns. The table contains illustrations on how the rows are combined (shades of red / orange / yellow) and how columns are combined (shades of gray and light blue). The syntax of the function name does first describe the operation on the rows (e.g. table merge) followed by the operation on the columns (e.g. table merge extend columns()). If no extension like ... extend columns is specified, then no additional columns are added in the target table and the data in the source table not fitting in the target table structure will not be taken over.


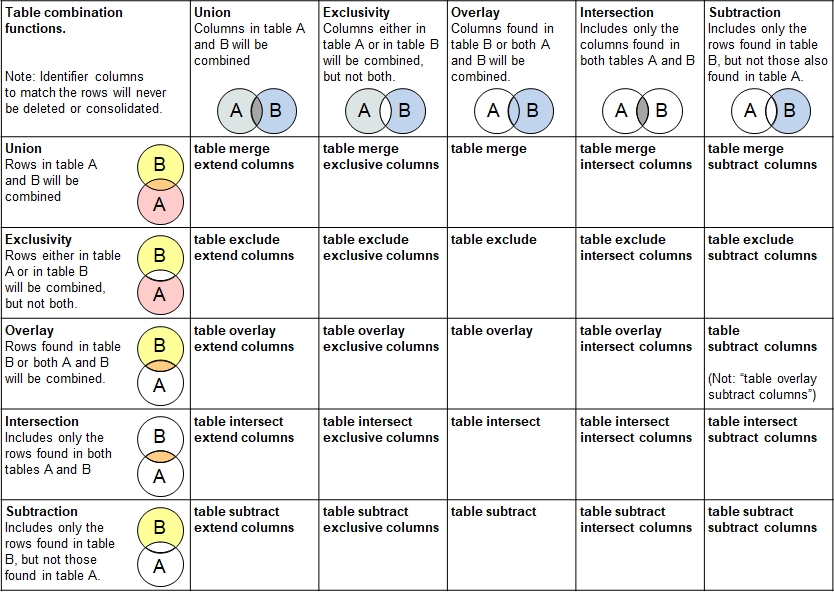
The term exclusivity is also known as symmetric difference and disjunctive union.

Additional Functions

Following table operations are also described in this section:

• Multiplying tables
• Dividing tables (binary division in relational algebra)
• Arranging tables sideways.

---

Procedures and Functions Provided:

Merge two tables with union-set principle:
    table merge
    table merge exclusive columns
    table merge extend columns
    table merge intersect columns
    table merge subtract columns

Table overlays the other table:
    table overlay
    table overlay columns
    table overlay exclusive columns
    table overlay extend columns
    table overlay intersect columns

Row-wise intersection made from two tables:
    table intersect
    table intersect columns
    table intersect exclusive columns
    table intersect extend columns
    table intersect intersect columns

One table does row-subtraction on other table:
    table subtract
    table subtract columns
    table subtract exclusive columns
    table subtract extend columns
    table subtract subtract columns

Derive disjoint union from both tables:
    table exclude
    table exclude columns
    table exclude exclude columns
    table exclude exclusive columns
    table exclude extend columns

Relational multiplication of two tables:
    table multiply
    table multiply selected rows

Relational division of two tables:
    table divide
    table divide selected rows

Arrange multiple tables side-by-side:
    table arrange
    table arrange with spacing