参考

1. Defective Majorana zero modes in non-Hermitian Kitaev chain（2021）arxiv.2010.11451

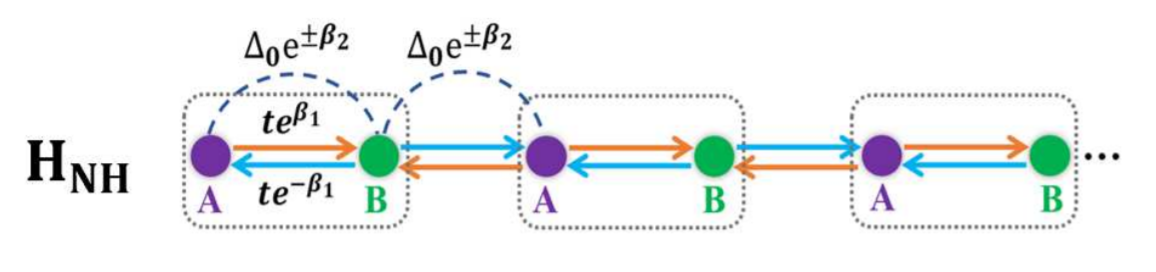
在普通的Kitaev基础上，引入

1. 非对称的跃迁幅度，向左向右分别是 $t_{L / R}=t e^{\pm \epsilon {\beta}_{1}}$
2. 非对称的超导配对，$\Delta^{\pm}=\Delta_{0} e^{\pm \beta_{2}}$

所以系统的哈密顿量变成 $\begin{aligned} H_{ NH }=&-\sum_{j}\left[t_{L} c_{j}^{\dagger} c_{j+1}+t_{R} c_{j+1}^{\dagger} c_{j}\right.\\ &\left.+\Delta^{+} c_{j}^{\dagger} c_{j+1}^{\dagger}+\Delta^{-} c_{j+1} c_{j}+\mu\left(1-2 n_{j}\right)\right] \end{aligned}$ 把哈密顿量写成BdG形式 $H_{ NH }=C^{\dagger} h_{ BdG } C$ 其中基底是 $\begin{aligned} C &=\left(c_{1, A}, \cdots, c_{N, B}, c_{1, A}^{\dagger}, \cdots, c_{N, B}^{\dagger}\right)^{T} \\ C^{\dagger} &=\left(c_{1, A}^{\dagger}, \cdots, c_{N, B}^{\dagger}, c_{1, A}, \cdots, c_{N, B}\right) \end{aligned}$