1. Graphene like
- 先计算石墨烯的基本模型,二次量子化紧束缚模型最近邻跃迁
- 加入次近邻跃迁,不需要磁场也能打破时间反演对称性,得到Haldane模型(Anomalous Quantum Hall effect)
- Haldane模型通过打破时间反演对称性得到非平庸拓扑态,现在我们想保留时间反演对称性下找到非平庸的拓扑态。有一种方法是把两个Haldane模型叠加在一起,得到了Kane-Mele模型(Spin Quantum Hall effect)
2. Tight-Binding Approximation for graphene
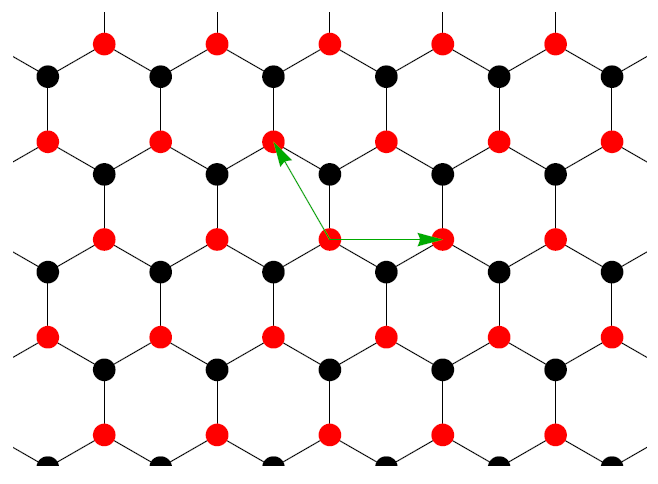
图中绿色的向量 v1 和 v2. 作为基底,其他晶格上的原子可以用 mv1+nv2 表示
- v1=(3a,0)
- v2=(−3/2a,3/2a).
每个单位元胞有两种子晶格
只考虑最近邻跃迁(nearest-neighbor (NN)),哈密顿量可以写成
H=−ti,j∑ai†bj−ti,j∑bi†aj
对于一个晶格,跃迁出去的有三种
- 沿着x轴旋转 θ=π/2, e1=(0,a)
- 沿着x轴旋转 θ=π/2+2π/3=7π/6,e2=(−23a,−2a)
- 沿着x轴旋转 θ=π/2+4π/3=11π/6, e3=(23a,−2a)
哈密顿量可以具体写成
H=−ti∑tbri+e1−ti∑bri−e2−tar+∑+bri+e3+h.c
2.1. 动量空间
傅里叶变换到动量空间
ak=N1i∑aieik⋅rai=N1k∑ake−ik⋅rbk=N1i∑aieik⋅rbi=N1k∑ake−ik⋅r
第一项变成
−ti∑ari†bri+e1=−Nti∑k∑k′∑ak†eik⋅ribk′e−ik⋅(ri+e1)=−tk∑k′∑ak†bk′e−ik⋅e1N1i∑ei(k−k′)ri=−tk∑k′∑ak†bk′e−ik⋅e1δk,k′=−tk∑ak†bke−ik⋅e1
类似的,计算另外两项
H=−ti∑ari†bri+e1−ti∑ari†bri+e2−ti∑ari†bri+e3+h.c.=−tk∑ak†bk(e−ik⋅e1+e−ik⋅e2+e−ik⋅e3)−tk∑bk†ak(eik⋅e1+eik⋅e2+eik⋅e3)=k∑(ak†bk†)(0H21(k)H12(k)0)(akbk)
其中
H12(k)=−t[exp(−ik⋅e1)+exp(−ik⋅e2)+exp(−ik⋅e3))H21(k)=H12(k)∗=−t[exp(ik⋅e1)+exp(ik⋅e2)+exp(ik⋅e3)]
矩阵
H(k)=(0H21(k)H12(k)0)
本征值
ϵ±(k)==±∣∣∣H12(k)∣∣∣±∣t∣3+2cos(3kxa)+4cos(23kxa)cos(23kya)
2.2. 闭合点
色散 ϵ± 是 k 空间的周期性函数。
- 低带 ϵ− 的最小值在 k=0.
- 低带 ϵ− 的最大值在布里渊区的六角晶格的角上。
六角晶格有六个角,但是
- θ=0,θ=2π/3 ,θ=4π/3 三个点是等价的点
- θ=π,θ=π+2π/3 ,θ=π+4π/3 三个点是等价的点
分别标记为
KK′=(33a4π,0)=(−33a4π,0)
在这些点上, ϵ+=ϵ−=0
ϵ±(K)=±∣∣∣H12(K)∣∣∣=±∣t∣3+2cos(3kxa)+4cos(23kxa)cos(23kya)=±∣t∣(3+2cos(333a4πa)+4cos(2333a4π)cos(23×0))=±∣t∣3+2cos(34π)+4cos(32π)=±∣t∣3+2×(−21)+4×(−21)=3−3=0
所以两个能带在这六个点上相交
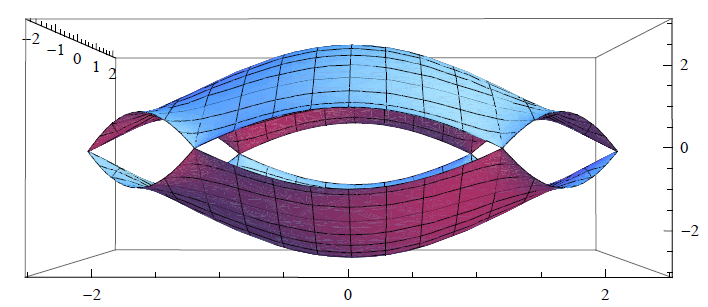
2.3. Dirac 点
在 K 和 K′ 点上,对色散线性化 ϵ±∝±(k−K).
ϵ±(k)=ϵ±(K+q)=±∣t∣(3+2cos[3(33a4π+qx)a]+4cos[23(33a4π+qx)a]cos(23qya))=±23∣t∣aqx2+qy2+O(q2)=±23∣t∣aq+O(q2)
画出图像
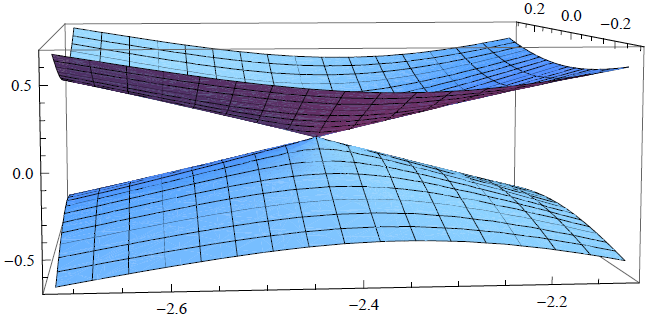
在 K 点附近
H(k)=H(K+q)=23ta(0qx+iqyqx−iqy0)+O(q2)≈23ta(qxσx+qyσy)=cq⋅σ
在 K′ 点附近
H(k)=H(K′+q)=−23ta(0qx−iqyqx+iqy0)+O(q2)≈−23ta(qxσx−qyσy)=−cq⋅(σxσσx)
其中 c 是光速
- 每个 K 或 K′ 点是一个外尔费米子
- K 和 K′ 两个外尔费米子,有不同的手征,合成一个狄拉克费米子
符合狄拉克方程
i∂tψ=(0cq⋅σcq⋅σ0)ψ


