参考文献
F. D. M. Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly" Phys. Rev. Lett. 61, 2015-2018 (1988).
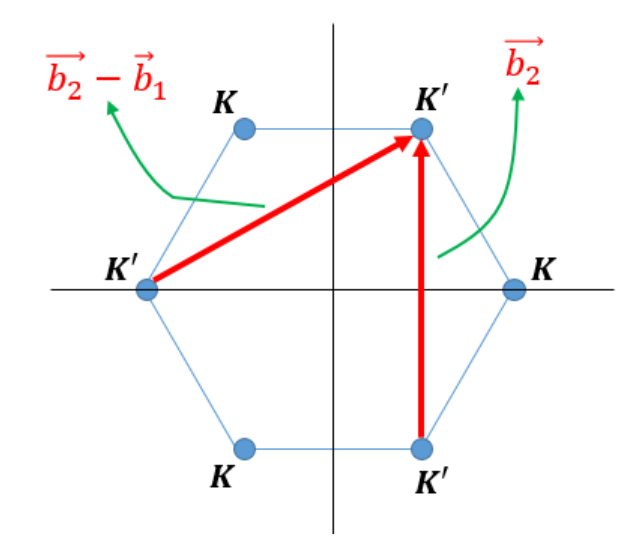
加入第二邻近跃迁
这个第二邻近跃迁又称为Haldane项,用m m m H m = m ∑ i C R i , 1 † C R i , 1 − C R i , 2 † C R i , 2 = − m ∑ i , σ ( − 1 ) σ C R i , σ † C R i , σ = − m ∑ k , σ ( − 1 ) σ C k , σ † C k , σ = ∑ k ( C k , 1 † C k , 2 † ) m σ z ( C k , 1 C k , 2 )
\begin{aligned}
H_{m} &=m \sum_{i} C_{ R _{i}, 1}^{\dagger} C_{ R _{i}, 1}-C_{ R _{i}, 2}^{\dagger} C_{ R _{i}, 2} \\
&=-m \sum_{i, \sigma}(-1)^{\sigma} C_{ R _{i}, \sigma}^{\dagger} C_{ R _{i}, \sigma} \\
&=-m \sum_{ k , \sigma}(-1)^{\sigma} C_{ k , \sigma}^{\dagger} C_{ k , \sigma} \\
&=\sum_{ k }\left(\begin{array}{ll}
C_{ k , 1}^{\dagger} & C_{ k , 2}^{\dagger}
\end{array}\right) m \sigma_{z}\left(\begin{array}{l}
C_{ k , 1} \\
C_{ k , 2}
\end{array}\right)
\end{aligned}
H m = m i ∑ C R i , 1 † C R i , 1 − C R i , 2 † C R i , 2 = − m i , σ ∑ ( − 1 ) σ C R i , σ † C R i , σ = − m k , σ ∑ ( − 1 ) σ C k , σ † C k , σ = k ∑ ( C k , 1 † C k , 2 † ) m σ z ( C k , 1 C k , 2 ) H ( k ) = H T B ( k ) + H m ( k )
H( k )=H_{T B}( k )+H_{m}( k )
H ( k ) = H T B ( k ) + H m ( k )
在泡利矩阵表示下的Haldane模型
H ( k , ϕ ) = h ( k , ϕ ) ⋅ σ
H( k , \phi)= h ( k , \phi) \cdot \sigma
H ( k , ϕ ) = h ( k , ϕ ) ⋅ σ h x = t 1 [ cos ( 3 3 k y ) + 2 cos ( k x 2 ) cos ( 3 6 k y ) ] h y = t 1 [ sin ( 3 3 k y ) − 2 cos ( k x 2 ) sin ( 3 6 k y ) ] h z = m + 2 t 2 sin ϕ [ sin ( k x ) − 2 sin ( k x 2 ) cos ( 3 2 k y ) ]
\begin{array}{l}
h_{x}=t_{1}\left[\cos \left(\frac{\sqrt{3}}{3} k_{y}\right)+2 \cos \left(\frac{k_{x}}{2}\right) \cos \left(\frac{\sqrt{3}}{6} k_{y}\right)\right] \\
h_{y}=t_{1}\left[\sin \left(\frac{\sqrt{3}}{3} k_{y}\right)-2 \cos \left(\frac{k_{x}}{2}\right) \sin \left(\frac{\sqrt{3}}{6} k_{y}\right)\right] \\
h_{z}=m+2 t_{2} \sin \phi\left[\sin \left(k_{x}\right)-2 \sin \left(\frac{k_{x}}{2}\right) \cos \left(\frac{\sqrt{3}}{2} k_{y}\right)\right]
\end{array}
h x = t 1 [ cos ( 3 3 k y ) + 2 cos ( 2 k x ) cos ( 6 3 k y ) ] h y = t 1 [ sin ( 3 3 k y ) − 2 cos ( 2 k x ) sin ( 6 3 k y ) ] h z = m + 2 t 2 sin ϕ [ sin ( k x ) − 2 sin ( 2 k x ) cos ( 2 3 k y ) ]
对于 K K K ( k x , k y ) = ( 4 π 3 , 0 ) \left(k_{x}, k_{y}\right)=\left(\frac{4 \pi}{3}, 0\right) ( k x , k y ) = ( 3 4 π , 0 )
展开 sin ( k x 2 ) ≈ 3 2 − 1 4 q x \sin \left(\frac{k_{x}}{2}\right) \approx \frac{\sqrt{3}}{2}-\frac{1}{4} q_{x} sin ( 2 k x ) ≈ 2 3 − 4 1 q x
展开 cos ( 3 2 k y ) ≈ 1 \cos \left(\frac{\sqrt{3}}{2} k_{y}\right) \approx 1 cos ( 2 3 k y ) ≈ 1
展开 sin k x ≈ − 3 2 − 1 2 q x \sin k_{x} \approx-\frac{\sqrt{3}}{2}-\frac{1}{2} q_{x} sin k x ≈ − 2 3 − 2 1 q x
其中 q x = k x − 4 π 3 q_{x}=k_{x}-\frac{4 \pi}{3} q x = k x − 3 4 π
所以哈密顿量在 K K K H K ≈ − t 1 3 2 ( q x σ x − q y σ y ) + ( m − 3 3 t 2 sin ϕ ) σ z
H_{K} \approx-\frac{t_{1} \sqrt{3}}{2}\left(q_{x} \sigma_{x}-q_{y} \sigma_{y}\right)+\left(m-3 \sqrt{3} t_{2} \sin \phi\right) \sigma_{z}
H K ≈ − 2 t 1 3 ( q x σ x − q y σ y ) + ( m − 3 3 t 2 sin ϕ ) σ z K ′ K^{\prime} K ′ ( k x , k y ) = ( − 4 π 3 , 0 ) \left(k_{x}, k_{y}\right)=\left(-\frac{4 \pi}{3}, 0\right) ( k x , k y ) = ( − 3 4 π , 0 ) H K ′ ≈ − t 1 3 2 ( q x σ x + q y σ y ) + ( m + 3 3 t 2 sin ϕ ) σ z
H_{K^{\prime}} \approx-\frac{t_{1} \sqrt{3}}{2}\left(q_{x} \sigma_{x}+q_{y} \sigma_{y}\right)+\left(m+3 \sqrt{3} t_{2} \sin \phi\right) \sigma_{z}
H K ′ ≈ − 2 t 1 3 ( q x σ x + q y σ y ) + ( m + 3 3 t 2 sin ϕ ) σ z
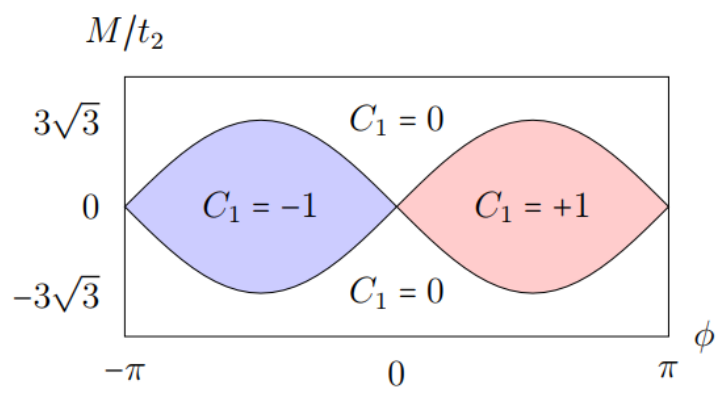
当 m ≈ − 3 3 t 2 sin ϕ m \approx-3 \sqrt{3} t_{2} \sin \phi m ≈ − 3 3 t 2 sin ϕ ϕ > 0 \phi>0 ϕ > 0
本征方程
( u − r e i θ − r e − i θ u ) ∣ − , k ⟩ = − E ∣ − , k ⟩
\left(\begin{array}{cc}
u & -r e^{i \theta} \\
-r e^{-i \theta} & u
\end{array}\right)|-, k\rangle=-E|-, k\rangle
( u − r e − i θ − r e i θ u ) ∣ − , k ⟩ = − E ∣ − , k ⟩
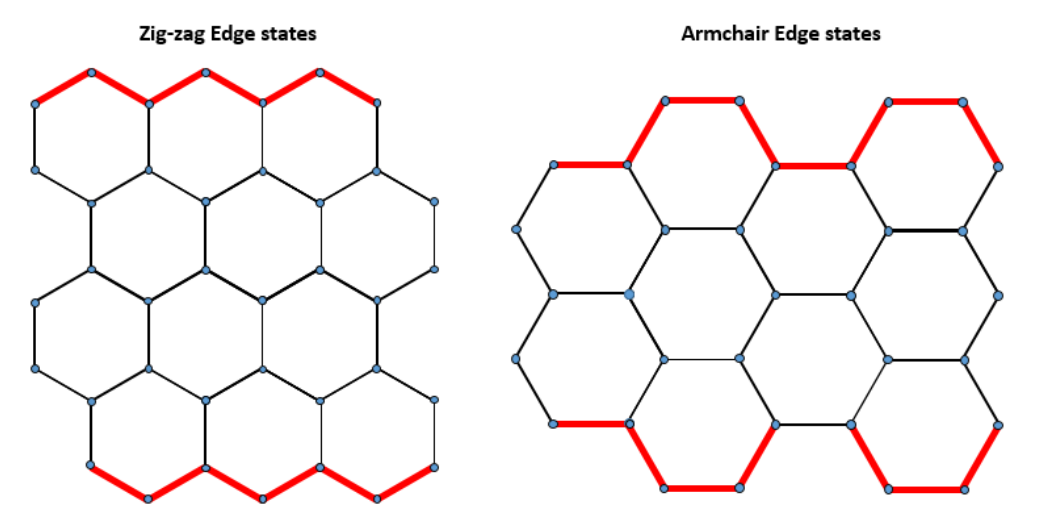
因为有非平庸拓扑数,我们可以预期存在边界态