1. Chapter02 SHH模型以及拓展

本章主题

1. 我先介绍SHH模型，一个关于电子在晶格跃迁的模型
2. 在SHH模型基础上加入位能(on-site potential)，得到Rice-Mele模型
3. 如果我们加入的位能是复数形式，于是我们把SHH模型拓展到非厄密形式
4. Rice-Mele模型的维度拓展到2维，得到Qi-Wu-Zhang模型

1.1. 参考文献

1. 《A Short Course on Topological Insulators: Band Structure and Edge States in One and Two Dimensions》 János K. Asbóth (2016)

2. SHH模型

SHH模型的哈密顿量 $H=\sum_{j=1}^{2 N}\left(\frac{t_{o}}{2}+(-1)^{j} \frac{\delta}{2}\right)\left(c_{j}^{\dagger} c_{j+1}+\text { h.c. }\right)$ 新的标记方式

• $c_{j}$ 湮灭子晶格A的电子
• $d_{j}$ 湮灭子晶格B的电子

SHH模型的哈密顿量可以写成 $H=\frac{1}{2} \sum_{j}^{N} \underbrace{\left(t_{o}-\delta\right)\left(c_{j}^{\dagger} d_{j}+\text { h.c. }\right)}_{\text {intracell hopping }}+\underbrace{\left(t_{o}+\delta\right)\left(c_{j+1}^{\dagger} d_{j}+\text { h.c. }\right)}_{\text {intercell hopping }}$

2.1. 实空间能谱

跃迁幅度标记为

• $v=t_{o}-\delta$
• $w=t_{o}+\delta$

SHH模型的哈密顿量可以写成 $\begin{aligned} H&=\frac{1}{2} \sum_{j}^{N} \underbrace{v\left(c_{j}^{\dagger} d_{j}+\text { h.c. }\right)}_{\text {intracell hopping }}+\underbrace{w\left(c_{j+1}^{\dagger} d_{j}+\text { h.c. }\right)}_{\text {intercell hopping }} \\ &=\left[\begin{array}{ll} A^{\dagger} & B^{\dagger} \end{array}\right]\left[\begin{array}{cc} 0 & H_{A B} \\ H_{A B}^{T} & 0 \end{array}\right]\left[\begin{array}{c} A \\ B \end{array}\right] \end{aligned}$ 哈密顿量对应的薛定谔方程 $\hat{H}_{\mathrm{bulk}}\left|\Psi_{n}(k)\right\rangle= E_{n}(k)\left|\Psi_{n}(k)\right\rangle$

不含时间情况下，就是本征方程，写成矩阵形式 $\left(\begin{array}{llllllll}{0} & {v} & {0} & {0} & {0} & {0} & {0} & {w} \\ {v} & {0} & {w} & {0} & {0} & {0} & {0} & {0} \\ {0} & {w} & {0} & {v} & {0} & {0} & {0} & {0} \\ {0} & {0} & {v} & {0} & {w} & {0} & {0} & {0} \\ {0} & {0} & {0} & {w} & {0} & {v} & {0} & {0} \\ {0} & {0} & {0} & {0} & {v} & {0} & {w} & {0} \\ {0} & {0} & {0} & {0} & {0} & {w} & {0} & {v} \\ {w} & {0} & {0} & {0} & {0} & {0} & {v} & {0}\end{array}\right)\left(\begin{array}{l}{a(k) e^{i k}} \\ {b(k) e^{i k}} \\ {a(k) e^{2 i k}} \\ {b(k) e^{2 i k}} \\ {a(k) e^{3 i k}} \\ {b(k) e^{3 i k}} \\ {a(k) e^{N i k}} \\ {b(k) e^{N i k}}\end{array}\right)=E(k) \left(\begin{array}{l}{a(k) e^{i k}} \\ {b(k) e^{i k}} \\ {a(k) e^{2 i k}} \\ {b(k) e^{2 i k}} \\ {a(k) e^{3 i k}} \\ {b(k) e^{3 i k}} \\ {a(k) e^{N i k}} \\ {b(k) e^{N i k}}\end{array}\right)$ 对角化矩阵，得到本征值，固定 $w=1$ 改变参数 $v$，画出下图

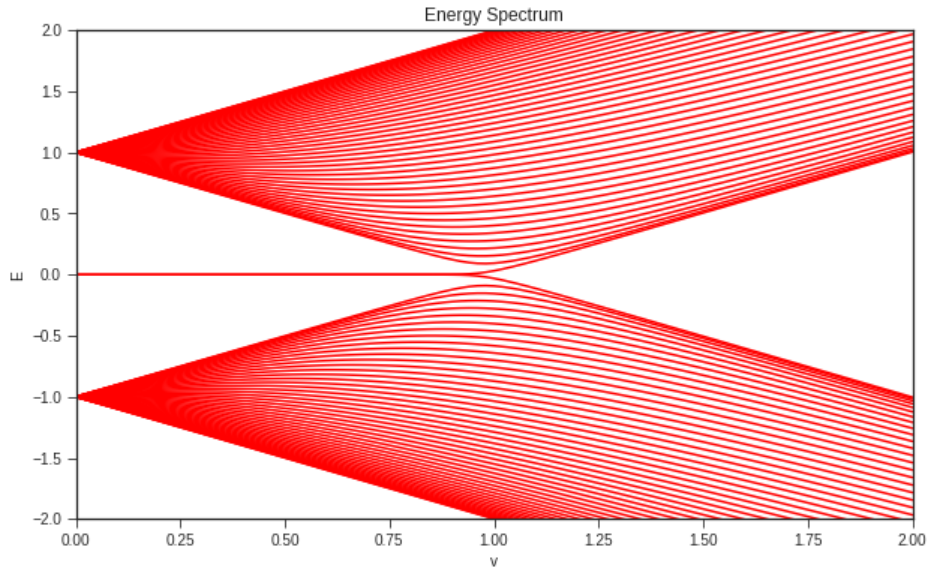
可以看出

1. 当 $v<w$ 时，存在一个能量为零的态。
2. 当 $v>w$ 时，能量为零的态消失。

为了弄清楚这个量为零的态，让我们进入动量空间，探索系统的性质。

2.2. k空间本征问题

傅里叶变换 $\begin{array}{l} c_{j}=\frac{1}{\sqrt{N}} \sum_{k} e^{i\left(j-\frac{1}{2}\right) k} c_{k} \\ d_{j}=\frac{1}{\sqrt{N}} \sum_{k} e^{i j k} d_{k} \end{array}$ SHH模型的实空间哈密顿量变成 $\begin{aligned} H=&\frac{1}{2 N} \sum_{ j , k , k ^{\prime}} \left(e^{-i\left(j-\frac{1}{2}\right) k+i j k^{\prime}} c_{k}^{\dagger} d_{k^{\prime}}+\text { h.c. }\right)\left(t_{o}-\delta\right) \\ &+\left(e^{-i\left(j+\frac{1}{2}\right) k+i j k^{\prime}} c_{k}^{\dagger} d_{k^{\prime}}+\text { h.c. }\right)\left(t_{o}+\delta\right) \\ =&\frac{1}{2 N} \sum_{ j , k , k ^{\prime}} \left(e^{i j\left(k^{\prime}-k\right)} e^{+i \frac{k}{2}} c_{k}^{\dagger} d_{k^{\prime}}+\text { h.c. }\right)\left(t_{o}-\delta\right) \\ &+\left(e^{i j\left(k^{\prime}-k\right)} e^{-i \frac{k}{2}} c_{k}^{\dagger} d_{k^{\prime}}+\text { h.c. }\right)\left(t_{o}+\delta\right)\\ =& \frac{1}{2} \sum_{ k }\left(c_{k}^{\dagger} d_{k} e^{+i \frac{k}{2}}+\text { h.c. }\right)\left(t_{o}-\delta\right) \\ &+\left(c_{k}^{\dagger} d_{k} e^{-i \frac{k}{2}}+\text { h.c. }\right)\left(t_{o}+\delta\right) \\ & \frac{1}{2} \sum_{k}\left[t_{o}\left(e^{+i \frac{k}{2}}+e^{-i \frac{k}{2}}\right)+\delta\left(e^{-i \frac{k}{2}}-e^{+i \frac{k}{2}}\right)\right] c_{k}^{\dagger} d_{k}+\text { h.c. } \\ =&\sum_{k}\left[t_{o} \cos \frac{k}{2}-i \delta \sin \frac{k}{2}\right] c_{k}^{\dagger} d_{k}+\text { h.c } \\ =&\sum_{k}\left(c_{k}^{\dagger} d_{k}^{\dagger}\right) \underbrace{\left(\begin{array}{cc} 0 & t_{o} \cos \frac{k}{2}-i \delta \sin \frac{k}{2} \\ t_{o} \cos \frac{k}{2}+i \delta \sin \frac{k}{2} & 0 \end{array}\right)}_{:=\tilde{H}(k)}\left(\begin{array}{l} c_{k} \\ d_{k} \end{array}\right) \end{aligned}$ 或者在新标记 $v=t_{o}-\delta$ 和 $w=t_{o}+\delta$ 下 $H(k)=\left(\begin{array}{cc} 0 & v+w e^{-i k} \\ v+w e^{i k} & 0 \end{array}\right)$ 矩阵的本征值，也就是色散关系 $E_{\pm}(k)=\pm \sqrt{v^{2}+w^{2}+2 v w \cos k}$ 对应的本征态 $\left|\psi_{+}\right\rangle=\frac{1}{\sqrt{2}}\left(\frac{E_{+}}{v+w e^{i k}}\right)$

$\left|\psi_{-}\right\rangle=\frac{1}{\sqrt{2}}\left(\frac{-E_{+}}{v+w e^{i k}}\right)$

2.2.1. 能谱

对于不同参数，色散关系 $E(k)=\pm\left|v+e^{-i k} w\right|=\pm \sqrt{v^{2}+w^{2}+2 v w \cos k}$ 作图

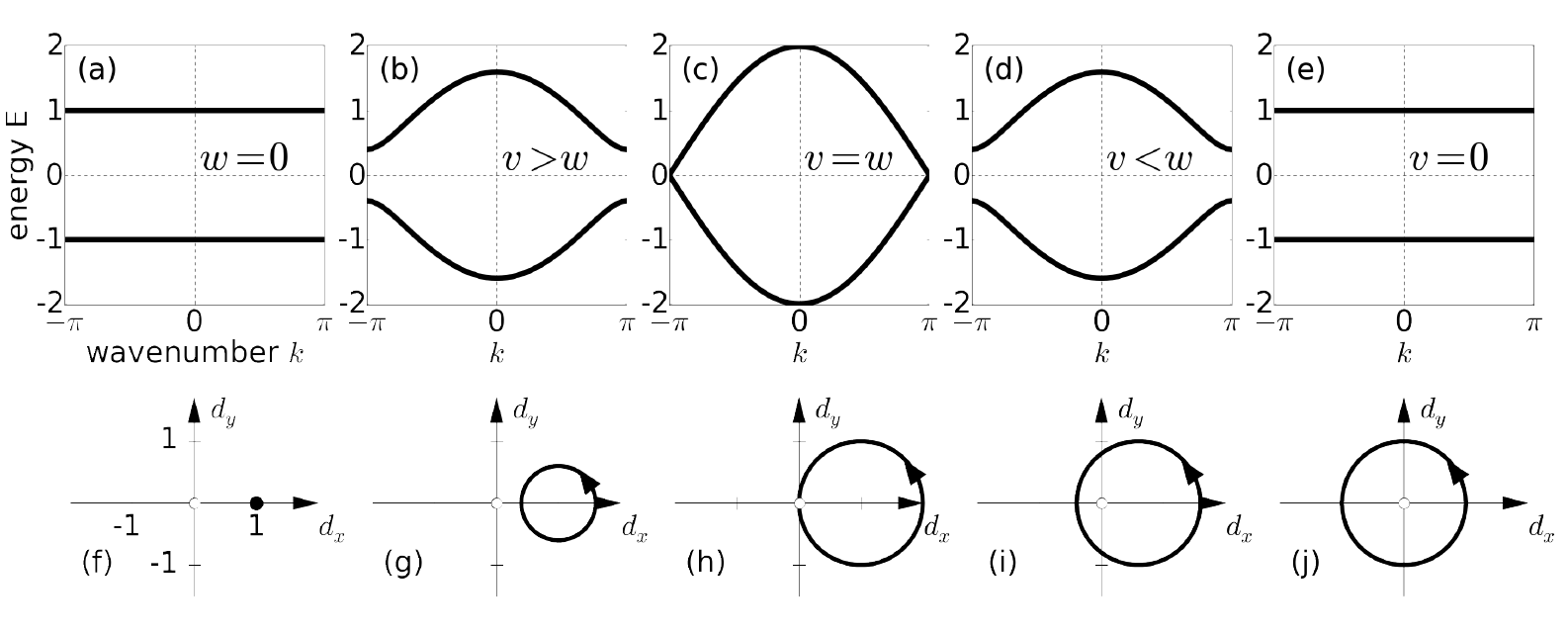
只要跳跃幅度不相等$v \neq w$，就会出现能量分裂（energy gap），满带和空带分开大小$2 \Delta$ $\Delta=\min _{k}|E(k)|=|v-w|$ 如果$v=w$，那么SHH就是描述导体了。平面波本征态之间能量可以任意小，物理上就是电子传输。

从参数变化的过程中，我们看到在 $v=w$ 的时候，系统经历了一次能隙的闭合打开。

一般来说能隙的闭合打开意味着发生相变，所以接下来计算贝利相位，一个可以描述系统拓扑的参数。

2.2.2. 贝利相位

经过闭合路径积分得到的贝利相位 $\gamma_{n}(C)=i \oint_{c}\left\langle n(R)\left|\nabla_{R}\right| n(R)\right\rangle \cdot d R$ 代入本征向量 $\begin{aligned} \gamma_{\pm}(k) &=i \int\left\langle\psi_{\pm}\left|\nabla_{k}\right| \psi_{\pm}\right) d k \\ &=\frac{i}{2} \int\left(\frac{E_{+}}{v+w e^{-i k}}\right) \frac{1}{d k}\left(\frac{E_{+}}{v+w e^{i k}}\right) d k \end{aligned}$ 对于不同参数 $\gamma=\left\{\begin{aligned} 0, \quad & \frac{w}{v}<1 \\ \pi, \quad & \frac{w}{v}>1 \end{aligned}\right.$

2.3. 边界态

接下来看看比较有观测意义的物理量。

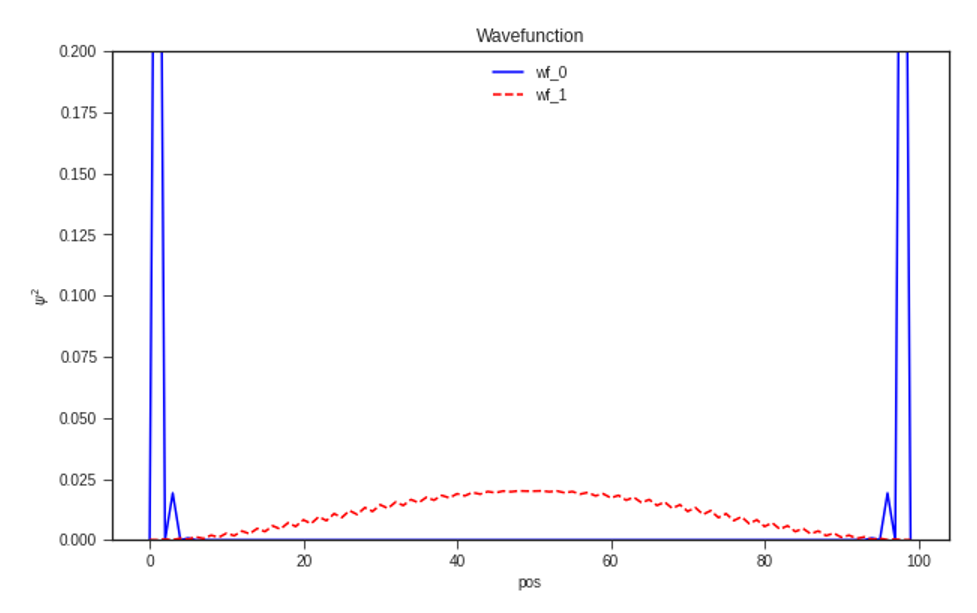
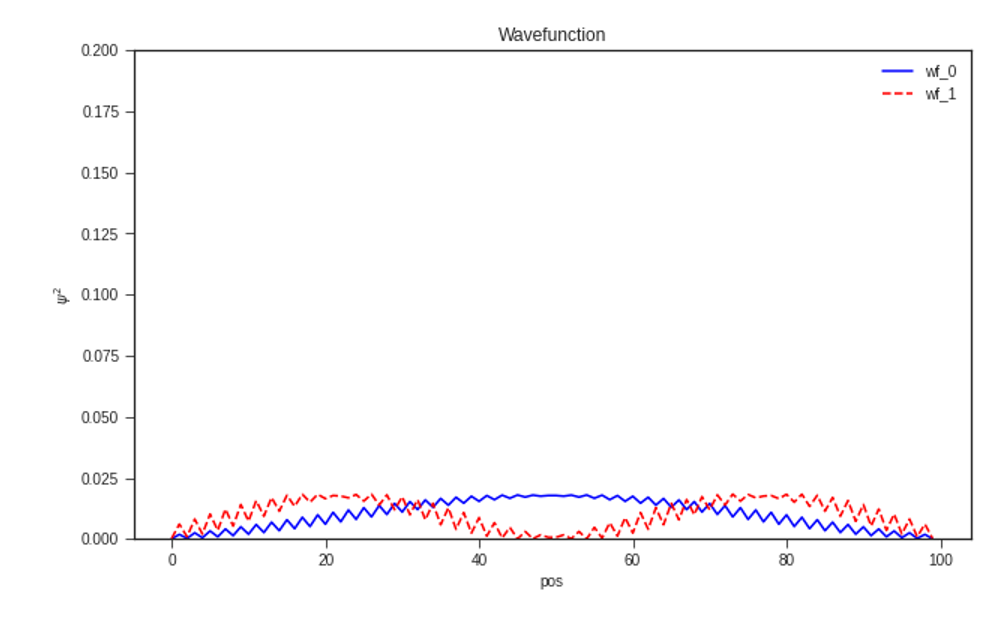
2.4. 纠缠谱

先构建系统的关联函数 $\begin{aligned}\left\langle a_{i}^{\dagger} a_{j}\right\rangle &=\frac{1}{2} \sum_{n, m=1}^{L / 2} V_{i, n} V_{j, m}\left\langle\left[\gamma_{n,+}^{\dagger}-\gamma_{n,-}^{\dagger}\right]\left[\gamma_{m,+}-\gamma_{m,-}\right]\right\rangle \\ &=\frac{1}{2} \sum_{n=1}^{L / 2} V_{i, n} V_{j, n}=\frac{1}{2} \delta_{i, j} \\\left\langle b_{i}^{\dagger} b_{j}\right\rangle &=\frac{1}{2} \sum_{n, m=1}^{L / 2} U_{i, n} U_{j, m}\left\langle\left[\gamma_{n,+}^{\dagger}+\gamma_{n,-}^{\dagger}\right]\left[\gamma_{m,+}+\gamma_{m,-}\right]\right\rangle \\ &=\frac{1}{2} \sum_{n=1}^{L / 2} U_{i, n} U_{j, n}=\frac{1}{2} \delta_{i, j} \\\left\langle a_{i}^{\dagger} b_{j}\right\rangle &=\frac{1}{2} \sum_{n, m=1}^{L / 2} V_{i, n} U_{j, m}\left\langle\left[\gamma_{n,+}^{\dagger}-\gamma_{n,-}^{\dagger}\right]\left[\gamma_{m,+}+\gamma_{m,-}\right]\right\rangle \\ &=-\frac{1}{2} \sum_{n=1}^{L / 2} V_{i, n} U_{j, n}=-\frac{1}{2}\left[V U^{T}\right]_{i j}=\left\langle b_{j}^{\dagger} a_{i}\right\rangle \end{aligned}$

把关联函数组合成一个关联矩阵 $\left[\begin{array}{ll} \left\langle a_{i}^{\dagger} a_{j}\right\rangle & \left\langle a_{i}^{\dagger} b_{j}\right\rangle \\ \left\langle b_{j}^{\dagger} a_{i}\right\rangle & \left\langle b_{i}^{\dagger} b_{j}\right\rangle \end{array}\right] =\left[\begin{array}{ll} \frac{1}{2} \delta_{i, j} & -\frac{1}{2}\left[V U^{T}\right]_{i j} \\ -\frac{1}{2}\left[V U^{T}\right]_{i j} & \frac{1}{2} \delta_{i, j} \end{array}\right]$

关联矩阵的大小是 $2 N_{A} * 2 N_{A}$

对角化关联矩阵，得到本征值 $\left\{\lambda_{i}, 1-\lambda_{i}\right\}$

这组本征值的分布就是纠缠谱(entanglement spectrum)

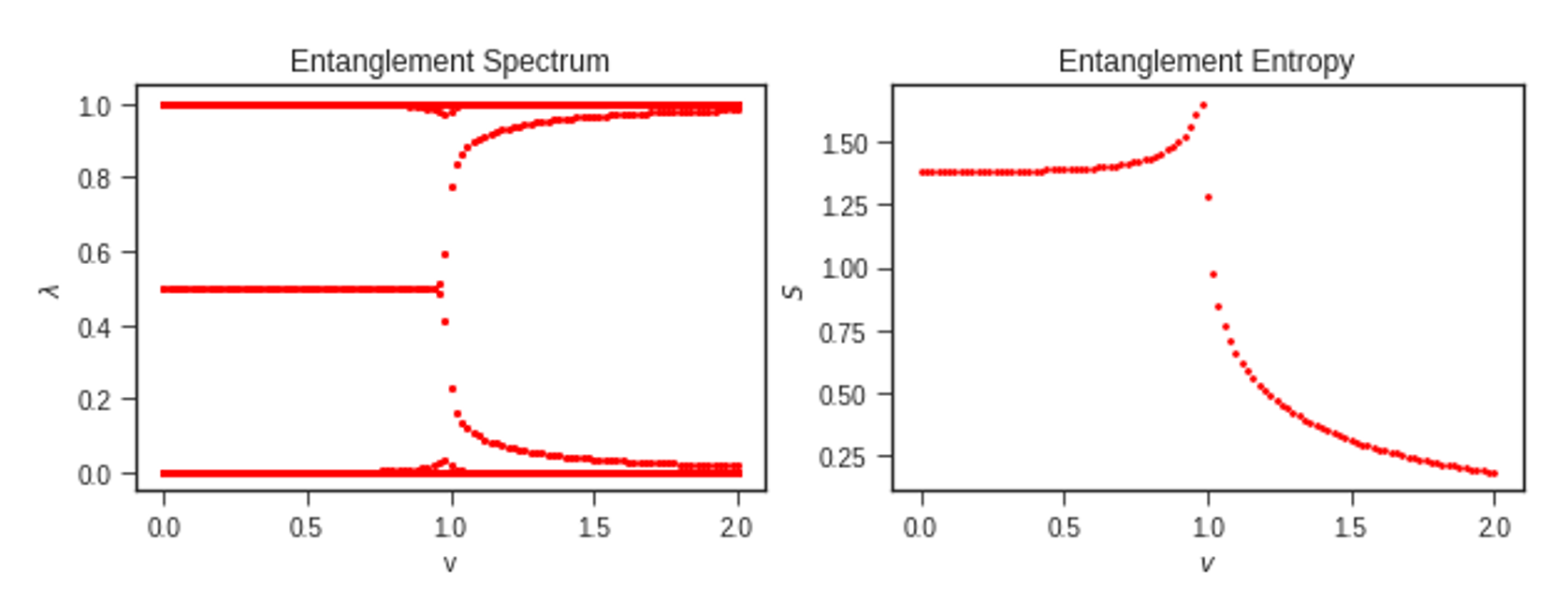
把纠缠谱用下面的公式计算出纠缠熵(entanglement entropy) $S_{A}=-\sum_{i}^{N_{A}}\left[\lambda_{i} \ln \lambda_{i}+\left(1-\lambda_{i}\right) \ln \left(1-\lambda_{i}\right)\right]$

可以看出，纠缠谱和纠缠熵在相变点 $v=w$ 都有奇异的行为。因此，可以根据这种行为来判断系统的拓扑性质是否发生相变。