• 模型
  • 哈密顿量
    • K算子
    • plaquettes算子
  • Majorana表示
    • Majorana算子
• 演生规范场

1. 模型

1.1. 哈密顿量

蜂窝六角晶格，在晶格每个顶点有自旋1/2的粒子。

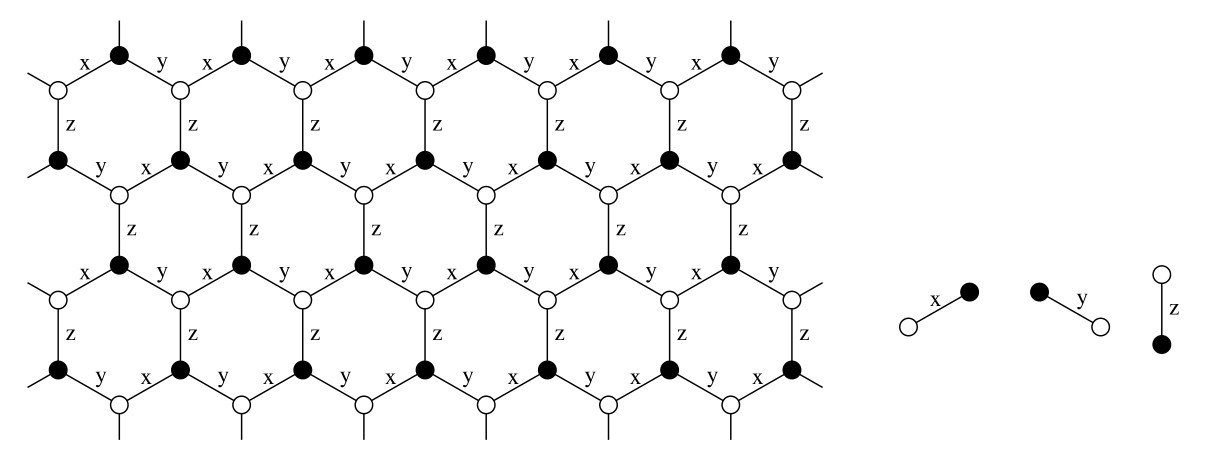
• 系统有两套子晶格，分别用黑色和白色表示。
• 自旋之间的连接，有三种类型
  1. x-型
  2. y-型
  3. z-型

模型哈密顿量 $H=-J_{x} \sum_{x \text {-links }} \sigma_{j}^{x} \sigma_{k}^{x}-J_{y} \sum_{y \text {-links }} \sigma_{j}^{y} \sigma_{k}^{y}-J_{z} \sum_{z \text {-links }} \sigma_{j}^{z} \sigma_{k}^{z} \text {, }$

1.1.1. K算子

哈密顿量有个简化的写法 $H=-\sum_{j \text { n.n. } k} J_{j k} K_{j k}$

其中算子 $K_{j k}=\left\{\begin{array}{ll} \sigma_{j}^{x} \sigma_{k}^{x}, & \text { if }(j, k) \text { is an } x \text {-link; } \\ \sigma_{j}^{x} \sigma_{k}^{y}, & \text { if }(j, k) \text { is an } y \text {-link; } \\ \sigma_{j}^{x} \sigma_{k}^{z}, & \text { if }(j, k) \text { is an } z \text {-link. } \end{array}\right.$

1.1.2. plaquettes算子

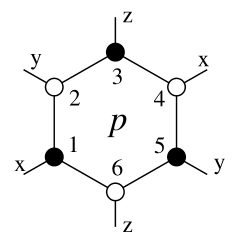
对于一个六边形的晶格，定义一个plaquettes算子 $\begin{aligned} W_{p}=&\sigma_{1}^{x} \sigma_{2}^{y} \sigma_{3}^{z} \sigma_{4}^{x} \sigma_{5}^{y} \sigma_{6}^{z} \\=&K_{12} K_{23} K_{34} K_{45} K_{56} K_{61} \end{aligned}$ plaquettes算子的对易关系 $\left[K_{i j}, W_{p}\right]=0$

$\left[H, W_{p}\right]=0$

$\left[W_{q}, W_{p}\right]=0$

因为这些对易关系，所有的plaquette定义了一组好量子数 $\left\{w_{p}\right\}$ ，而由 $W_{p}^{2}=1$ 可以得到其本征值 $w_{p}=\pm 1$ 。这组好量子数，将整个 $2^{N}$ 维希尔伯特空间分成了若干子空间 $H =\underset{w_{1}, \ldots, w_{m}}{\oplus} H _{w_{1}, \ldots, w_{m}}$

• 每个小的空间是$W_{p}$的本征空间。
• 对于 $n$ 个顶点的系统，里面有 $m=n / 2$ 个plaquettes算子。

1.2. Majorana表示

我们先用费米子算符代替自旋算符表示哈密顿量，然后换成用Majorana算符表示

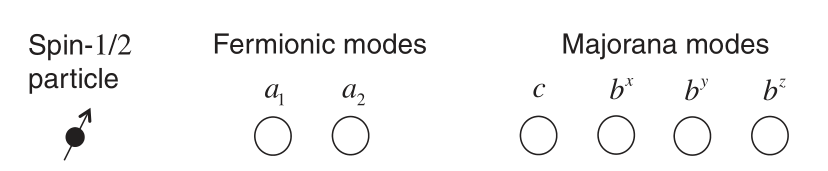
费米子算符$a_{k}, a_{k}^{\dagger}$可以拆分成实数部分和虚数部分 $a_{k}=c_{2 k-1}+ic_{2 k}$

$a_{k}^{\dagger}=c_{2 k-1}-ic_{2 k}$

实数部分和虚数部分被称为Majorana算子，表示成上式的逆变换 $c_{2 k-1}=a_{k}+a_{k}^{\dagger}$

$c_{2 k}=\frac{a_{k}-a_{k}^{\dagger}}{i}$

也就是Majorana算子表示成费米子算符$a_{k}, a_{k}^{\dagger}$的线性组合

Majorana算子 $c_{j}$ 定义了Clifford代数 $\left\{c_{i}, c_{j}\right\}=2 \delta_{i j}$

1.2.1. Majorana算子

2. 演生规范场