- Cover
- Acknowledgments
- 1 Preface
- 2 (R)e-Introduction to statistics
- 2.1 Histograms, boxplots, and density curves
- 2.2 Pirate-plots
- 2.3 Models, hypotheses, and permutations for the two sample mean situation
- 2.4 Permutation testing for the two sample mean situation
- 2.5 Hypothesis testing (general)
- 2.6 Connecting randomization (nonparametric) and parametric tests
- 2.7 Second example of permutation tests
- 2.8 Reproducibility Crisis: Moving beyond p < 0.05, publication bias, and multiple testing issues
- 2.9 Confidence intervals and bootstrapping
- 2.10 Bootstrap confidence intervals for difference in GPAs
- 2.11 Chapter summary
- 2.12 Summary of important R code
- 2.13 Practice problems
- 3 One-Way ANOVA
- 3.1 Situation
- 3.2 Linear model for One-Way ANOVA (cell-means and reference-coding)
- 3.3 One-Way ANOVA Sums of Squares, Mean Squares, and F-test
- 3.4 ANOVA model diagnostics including QQ-plots
- 3.5 Guinea pig tooth growth One-Way ANOVA example
- 3.6 Multiple (pair-wise) comparisons using Tukey’s HSD and the compact letter display
- 3.7 Pair-wise comparisons for the Overtake data
- 3.8 Chapter summary
- 3.9 Summary of important R code
- 3.10 Practice problems
- 4 Two-Way ANOVA
- 4.1 Situation
- 4.2 Designing a two-way experiment and visualizing results
- 4.3 Two-Way ANOVA models and hypothesis tests
- 4.4 Guinea pig tooth growth analysis with Two-Way ANOVA
- 4.5 Observational study example: The Psychology of Debt
- 4.6 Pushing Two-Way ANOVA to the limit: Un-replicated designs and Estimability
- 4.7 Chapter summary
- 4.8 Summary of important R code
- 4.9 Practice problems
- 5 Chi-square tests
- 5.1 Situation, contingency tables, and tableplots
- 5.2 Homogeneity test hypotheses
- 5.3 Independence test hypotheses
- 5.4 Models for R by C tables
- 5.5 Permutation tests for the \(X^2\) statistic
- 5.6 Chi-square distribution for the \(X^2\) statistic
- 5.7 Examining residuals for the source of differences
- 5.8 General protocol for \(X^2\) tests
- 5.9 Political party and voting results: Complete analysis
- 5.10 Is cheating and lying related in students?
- 5.11 Analyzing a stratified random sample of California schools
- 5.12 Chapter summary
- 5.13 Summary of important R commands
- 5.14 Practice problems
- 6 Correlation and Simple Linear Regression
- 6.1 Relationships between two quantitative variables
- 6.2 Estimating the correlation coefficient
- 6.3 Relationships between variables by groups
- 6.4 Inference for the correlation coefficient
- 6.5 Are tree diameters related to tree heights?
- 6.6 Describing relationships with a regression model
- 6.7 Least Squares Estimation
- 6.8 Measuring the strength of regressions: R2
- 6.9 Outliers: leverage and influence
- 6.10 Residual diagnostics – setting the stage for inference
- 6.11 Old Faithful discharge and waiting times
- 6.12 Chapter summary
- 6.13 Summary of important R code
- 6.14 Practice problems
- 7 Simple linear regression inference
- 7.1 Model
- 7.2 Confidence interval and hypothesis tests for the slope and intercept
- 7.3 Bozeman temperature trend
- 7.4 Randomization-based inferences for the slope coefficient
- 7.5 Transformations part I: Linearizing relationships
- 7.6 Transformations part II: Impacts on SLR interpretations: log(y), log(x), & both log(y) & log(x)
- 7.7 Confidence interval for the mean and prediction intervals for a new observation
- 7.8 Chapter summary
- 7.9 Summary of important R code
- 7.10 Practice problems
- 8 Multiple linear regression
- 8.1 Going from SLR to MLR
- 8.2 Validity conditions in MLR
- 8.3 Interpretation of MLR terms
- 8.4 Comparing multiple regression models
- 8.5 General recommendations for MLR interpretations and VIFs
- 8.6 MLR inference: Parameter inferences using the t-distribution
- 8.7 Overall F-test in multiple linear regression
- 8.8 Case study: First year college GPA and SATs
- 8.9 Different intercepts for different groups: MLR with indicator variables
- 8.10 Additive MLR with more than two groups: Headache example
- 8.11 Different slopes and different intercepts
- 8.12 F-tests for MLR models with quantitative and categorical variables and interactions
- 8.13 AICs for model selection
- 8.14 Case study: Forced expiratory volume model selection using AICs
- 8.15 Chapter summary
- 8.16 Summary of important R code
- 8.17 Practice problems
- 9 Case studies
- 9.1 Overview of material covered
- 9.2 The impact of simulated chronic nitrogen deposition on the biomass and N2-fixation activity of two boreal feather moss–cyanobacteria associations
- 9.3 Ants learn to rely on more informative attributes during decision-making
- 9.4 Multi-variate models are essential for understanding vertebrate diversification in deep time
- 9.5 What do didgeridoos really do about sleepiness?
- 9.6 General summary
- References
3.2 Linear model for One-Way ANOVA (cell-means and reference-coding)
We introduced the statistical model \(y_{ij} = \mu_j+\varepsilon_{ij}\) in Chapter 2 for the situation with \(j = 1 \text{ or } 2\) to denote a situation where there were two groups and, for the model that is consistent with the alternative hypothesis, the means differed. Now there are seven groups and the previous model can be extended to this new situation by allowing \(j\) to be 1, 2, 3, …, 7. As before, the linear model assumes that the responses follow a normal distribution with the model defining the mean of the normal distributions and all observations have the same variance. *Linear models assume that the parameters for the mean in the model enter linearly. This last condition is hard to explain at this level of material – it is sufficient to know that there are models where the parameters enter the model nonlinearly and that they are beyond the scope of this function and this material and you won’t run into them in most statistical models. By employing this general “linear” modeling methodology, we will be able to use the same general modeling framework for the methods in Chapters ??, ??, ??, ??, and ??.
As in Chapter 2, the null hypothesis defines a situation (and model) where all the groups have the same mean. Specifically, the null hypothesis in the general situation with \(J\) groups (\(J\ge 2\)) is to have all the \(\underline{\text{true}}\) group means equal,
\[H_0:\mu_1 = \ldots = \mu_J.\]
This defines a model where all the groups have the same mean so it can be defined in terms of a single mean, \(\mu\), for the \(i^{th}\) observation from the \(j^{th}\) group as \(y_{ij} = \mu+\varepsilon_{ij}\). This is not the model that most researchers want to be the final description of their study as it implies no difference in the groups. There is more caution required to specify the alternative hypothesis with more than two groups. The alternative hypothesis needs to be the logical negation of this null hypothesis of all groups having equal means; to make the null hypothesis false, we only need one group to differ but more than one group could differ from the others. Essentially, there are many ways to “violate” the null hypothesis so we choose some delicate wording for the alternative hypothesis when there are more than 2 groups. Specifically, we state the alternative as
\[H_A: \text{ Not all } \mu_j \text{ are equal}\]
or, in words, at least one of the true means differs among the J groups. You might be attracted to trying to say that all means are different in the alternative but we do not put this strict a requirement in place to reject the null hypothesis. The alternative model allows all the true group means to differ but does require that they are actually all different with the model written as
\[y_{ij} = {\color{red}{\mu_j}}+\varepsilon_{ij}.\]
This linear model states that the response for the \(i^{th}\) observation in the \(j^{th}\) group, \(\mathbf{y_{ij}}\), is modeled with a group \(j\) (\(j=1, \ldots, J\)) population mean, \(\mu_j\), and a random error for each subject in each group, \(\varepsilon_{ij}\), that we assume follows a normal distribution and that all the random errors have the same variance, \(\sigma^2\). We can write the assumption about the random errors, often called the normality assumption, as \(\varepsilon_{ij} \sim N(0,\sigma^2)\). There is a second way to write out this model that allows extension to more complex models discussed below, so we need a name for this version of the model. The model written in terms of the \({\color{red}{\mu_j}}\text{'s}\) is called the cell means model and is the easier version of this model to understand.
One of the reasons we learned about pirate-plots is that it helps us visually consider all the aspects of this model. In Figure 2.28, we can see the bold horizontal lines that provide the estimated (sample) group means. The bigger the differences in the sample means (especially relative to the variability around the means), the more evidence we will find against the null hypothesis. You can also see the null model on the plot that assumes all the groups have the same mean as displayed in the dashed horizontal line at 117.1 cm (the R code below shows the overall mean of Distance is 117.1). While the hypotheses focus on the means, the model also contains assumptions about the distribution of the responses – specifically that the distributions are normal and that all the groups have the same variability, which do not appear to be clearly violated in this situation.
## [1] 117.126There is a second way to write out the One-Way ANOVA model that provides a framework for extensions to more complex models described in Chapter ?? and beyond. The other parameterization (way of writing out or defining) of the model is called the reference-coded model since it writes out the model in terms of a baseline group and deviations from that baseline or reference level. The reference-coded model for the \(i^{th}\) subject in the \(j^{th}\) group is \(y_{ij} ={\color{purple}{\boldsymbol{\alpha + \tau_j}}}+\varepsilon_{ij}\) where \(\color{purple}{\boldsymbol{\alpha}}\) (“alpha”) is the true mean for the baseline group (usually first alphabetically) and the \(\color{purple}{\boldsymbol{\tau_j}}\) (tau \(j\)) are the deviations from the baseline group for group \(j\). The deviation for the baseline group, \(\color{purple}{\boldsymbol{\tau_1}}\), is always set to 0 so there are really just deviations for groups 2 through \(J\). The equivalence between the reference-coded and cell-means models can be seen by considering the mean for the first, second, and \(J^{th}\) groups in both models:
\[\begin{array}{lccc} & \textbf{Cell means:} && \textbf{Reference-coded:}\\ \textbf{Group } 1: & \color{red}{\mu_1} && \color{purple}{\boldsymbol{\alpha}} \\ \textbf{Group } 2: & \color{red}{\mu_2} && \color{purple}{\boldsymbol{\alpha + \tau_2}} \\ \ldots & \ldots && \ldots \\ \textbf{Group } J: & \color{red}{\mu_J} && \color{purple}{\boldsymbol{\alpha +\tau_J}} \end{array}\]
The hypotheses for the reference-coded model are similar to those in the cell-means coding except that they are defined in terms of the deviations, \({\color{purple}{\boldsymbol{\tau_j}}}\). The null hypothesis is that there is no deviation from the baseline for any group – that all the \({\color{purple}{\boldsymbol{\tau_j\text{'s}}}}=0\),
\[\boldsymbol{H_0: \tau_2=\ldots=\tau_J=0}.\]
The alternative hypothesis is that at least one of the deviations is not 0,
\[\boldsymbol{H_A:} \textbf{ Not all } \boldsymbol{\tau_j} \textbf{ equal } \bf{0}.\]
In this chapter, you are welcome to use either version (unless we instruct you
otherwise) but we have to use the reference-coding in subsequent chapters. The
next task is to learn how to use R’s linear model, lm, function to get
estimates of the parameters50 in each model, but first a quick review of these
new ideas:
Cell Means Version
\(H_0: {\color{red}{\mu_1= \ldots = \mu_J}}\) \(H_A: {\color{red}{\text{ Not all } \mu_j \text{ equal}}}\)
Null hypothesis in words: No difference in the true means among the groups.
Null model: \(y_{ij} = \mu+\varepsilon_{ij}\)
Alternative hypothesis in words: At least one of the true means differs among the groups.
Alternative model: \(y_{ij} = \color{red}{\mu_j}+\varepsilon_{ij}.\)
Reference-coded Version
\(H_0: \color{purple}{\boldsymbol{\tau_2 = \ldots = \tau_J = 0}}\) \(H_A: \color{purple}{\text{ Not all } \tau_j \text{ equal 0}}\)
Null hypothesis in words: No deviation of the true mean for any groups from the baseline group.
Null model: \(y_{ij} =\boldsymbol{\alpha} +\varepsilon_{ij}\)
Alternative hypothesis in words: At least one of the true deviations is different from 0 or that at least one group has a different true mean than the baseline group.
Alternative model: \(y_{ij} =\color{purple}{\boldsymbol{\alpha + \tau_j}}+\varepsilon_{ij}\)
In order to estimate the models discussed above, the lm function is used51. The lm function continues to
use the same format as previous functions and in Chapter 2 , lm(Y~X, data=datasetname).
It ends up that lm generates the reference-coded version of the
model by default (The developers of R thought it was that important!).
But we want to start with the
cell-means version of the model,
so we have to override the standard technique
and add a “-1” to the formula interface to tell R that we want to the
cell-means coding. Generally, this looks like lm(Y~X-1, data=datasetname).
Once we fit a model in R, the summary function run on the model provides a
useful “summary” of the model coefficients and a suite of other potentially
interesting information. For the moment, we will focus on the estimated model
coefficients, so only those lines are provided. When fitting the cell-means version
of the One-Way ANOVA model,
you will find a row of output for each group relating estimating the \(\mu_j\text{'s}\).
The output contains columns for an estimate (Estimate), standard error
(Std. Error), \(t\)-value (t value), and p-value (Pr(>|t|)). We’ll
explore which of these are of interest in these models below, but focus
on the estimates of the parameters that the function provides in the first
column (“Estimate”) of the coefficient table and compare these results to what was found using favstats.
## Estimate Std. Error t value Pr(>|t|)
## Conditioncasual 117.6110 1.071873 109.7248 0
## Conditioncommute 114.6079 1.021931 112.1484 0
## Conditionhiviz 118.4383 1.101992 107.4765 0
## Conditionnovice 116.9405 1.053114 111.0426 0
## Conditionpolice 122.1215 1.064384 114.7344 0
## Conditionpolite 114.0518 1.015435 112.3182 0
## Conditionracer 116.7559 1.024925 113.9164 0In general, we denote estimated parameters with a hat over the parameter of
interest to show that it is an estimate. For the true mean of group \(j\),
\(\mu_j\), we estimate it with \(\hat{\mu}_j\), which is just the sample mean for group
\(j\), \(\bar{x}_j\). The model suggests an estimate for each observation that we denote
as \(\hat{y}_{ij}\) that we will also call a fitted value based on the model
being considered. The
same estimate is used for all observations in the each group in this model. R tries to help you to
sort out which row of output corresponds to which group by appending the group name
with the variable name. Here, the variable name was Condition and the first group
alphabetically was casual, so R provides a row labeled Conditioncasual
with an estimate of 117.61. The sample means from the seven groups can be seen to
directly match the favstats results presented previously.
The reference-coded version of the same model is more complicated but ends up giving the same results once we understand what it is doing. It uses a different parameterization to accomplish this, so has different model output. Here is the model summary:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 117.6110398 1.071873 109.7247845 0.000000000
## Conditioncommute -3.0031051 1.480964 -2.0278039 0.042626835
## Conditionhiviz 0.8272234 1.537302 0.5381008 0.590528548
## Conditionnovice -0.6705193 1.502651 -0.4462242 0.655452292
## Conditionpolice 4.5104792 1.510571 2.9859423 0.002839115
## Conditionpolite -3.5591965 1.476489 -2.4105807 0.015958695
## Conditionracer -0.8551713 1.483032 -0.5766371 0.564207492The estimated model coefficients are \(\hat{\alpha} = 117.61\) cm, \(\hat{\tau}_2 =-3.00\) cm, \(\hat{\tau}_3=0.83\) cm, and so on up to \(\hat{\tau}_7=-0.86\) cm, where R selected group 1 for casual, 2 for commute, 3 for hiviz, all the way up to group 7 for racer. The way you can figure out the baseline group (group 1 is casual here) is to see which category label is not present in the reference-coded output. The baseline level is typically the first group label alphabetically, but you should always check this52. Based on these definitions, there are interpretations available for each coefficient. For \(\hat{\alpha} = 117.61\) cm, this is an estimate of the mean overtake distance for the casual outfit group. \(\hat{\tau}_2 =-3.00\) cm is the deviation of the commute group’s mean from the causal group’s mean (specifically, it is \(3.00\) cm lower and was a quantity we explored in detail in Chapter 2 when we just focused on comparing casual and commute groups). \(\hat{\tau}_3=0.83\) cm tells us that the hiviz group mean distance is 0.83 cm higher than the casual group mean and \(\hat{\tau}_3=-0.86\) says that the racer sample mean was 0.86 cm lower than for the casual group. These interpretations are interesting as they directly relate to comparisons of groups with the baseline and lead directly to reconstructing the estimated means for each group by combining the baseline and a pertinent deviation as shown in Table 2.3.
(ref:tab3-1) Constructing group mean estimates from the reference-coded linear model estimates.
| Group | Formula | Estimates |
|---|---|---|
| casual | \(\hat{\alpha}\) | 117.61 cm |
| commute | \(\hat{\alpha}+\hat{\tau}_2\) | 117.61 - 3.00 = 114.61 cm |
| hiviz | \(\hat{\alpha}+\hat{\tau}_3\) | 117.61 + 0.82 = 118.43 cm |
We can also visualize the results of our linear models using what are called
term-plots or effect-plots
(from the effects package; (Fox et al. 2019))
as displayed in Figure 2.29. We don’t want to use the word
“effect” for these model components unless we have random assignment in the study
design so we generically call these term-plots as they display terms or
components from the model in hopefully useful ways to aid in model interpretation
even in the presence of complicated model parameterizations. The word “effect” has a causal connotation that we want to avoid as much as possible in non-causal (so non-randomly assigned) situations. Term-plots take an estimated model and show you its estimates along with 95% confidence
intervals generated by the linear model. These confidence intervals may differ from the confidence intervals in the pirate-plots since the pirate-plots make them for each group separately and term-plots are combining information across groups via the estimated model and then doing inferences for individual group means. To make term-plots, you need to install and
load the effects package and then use plot(allEffects(...)) functions
together on the lm object called lm2 that was estimated above. You can
find the correspondence between the displayed means and the estimates that were
constructed in Table 2.3.
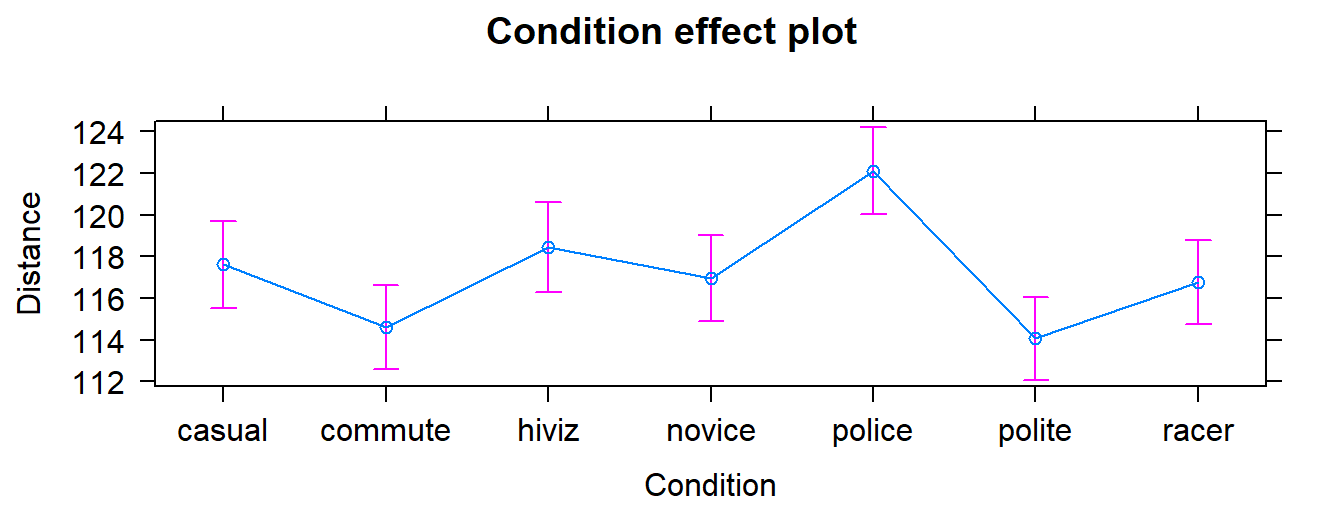
Figure 2.29: Plot of the estimated group mean distances from the reference-coded model for the overtake data from the effects package.
In order to assess overall evidence against having the same means for the all groups (vs not having the same means), we
compare either of the previous models (cell-means or reference-coded) to a null
model based on the null hypothesis of \(H_0: \mu_1 = \ldots = \mu_J\), which implies a
model of \(\color{red}{y_{ij} = \mu+\varepsilon_{ij}}\) in the cell-means version
where \({\color{red}{\mu}}\) is a common mean for all the observations. We will call
this the mean-only model since it only has a single mean
in it. In the reference-coded version of the model, we have a null hypothesis of
\(H_0: \tau_2 = \ldots = \tau_J = 0\), so the “mean-only” model is
\(\color{purple}{y_{ij} =\boldsymbol{\alpha}+\varepsilon_{ij}}\) with
\(\color{purple}{\boldsymbol{\alpha}}\) having the same definition as
\(\color{red}{\mu}\) for the cell-means model – it forces a common value for the
mean for all the groups. Moving from the reference-coded model to the mean-only
model is also an example of a situation where we move from a “full” model
to a
“reduced” model by setting some coefficients in the “full” model to 0 and, by doing
this, get a simpler or “reduced” model.
Simple models can be good as they are easier
to interpret, but having a model for \(J\) groups that suggests no difference in the
groups is not a very exciting result
in most, but not all, situations53. In order for R to provide
results for the mean-only model, we remove the grouping variable, Condition, from
the model formula and just include a “1”. The (Intercept) row of the output
provides the estimate for the mean-only model as a reduced model from either the
cell-means or reference-coded models when we assume that the mean is the same
for all groups:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 117.126 0.3977533 294.469 0This model provides an estimate of the common mean for all observations of \(117.13 = \hat{\mu} = \hat{\alpha}\) cm. This value also is the dashed horizontal line in the pirate-plot in Figure 2.28. Some people call this mean-only model estimate the “grand” or “overall” mean and notationally is represented as \(\bar{\bar{y}}\).
References
Fox, John, Sanford Weisberg, Brad Price, Michael Friendly, and Jangman Hong. 2019. Effects: Effect Displays for Linear, Generalized Linear, and Other Models. https://CRAN.R-project.org/package=effects.
In Chapter 2, we used
lmto get these estimates and focused on the estimate of the difference between the second group and the baseline - that was and still is the difference in the sample means. Now there are potentially more than two groups and we need to formalize notation to handle this more complex sitation.↩If you look closely in the code for the rest of the book, any model for a quantitative response will use this function, suggesting a common thread in the most commonly used statistical models.↩
We can and will select the order of the levels of categorical variables as it can make plots easier to interpret.↩
Suppose we were doing environmental monitoring and were studying asbestos levels in soils. We might be hoping that the mean-only model were reasonable to use if the groups being compared were in remediated areas and in areas known to have never been contaminated.↩