7.7 Confidence interval for the mean and prediction intervals for a new observation

Figure 2.131 provided a term-plot of the estimated regression line and a shaded area surrounding the estimated regression equation. Those shaded areas are based on connecting the dots on 95% confidence intervals constructed for the true mean \(y\) value across all the x-values. To formalize this idea, consider a specific value of \(x\), and call it \(\boldsymbol{x_{\nu}}\) (pronounced x-new¹¹⁰). Then the true mean response for this subpopulation (a subpopulation is all observations we could obtain at \(\boldsymbol{x=x_{\nu}}\)) is given by \(\boldsymbol{E(Y)=\mu_\nu=\beta_0+\beta_1x_{\nu}}\). To estimate the mean response at \(\boldsymbol{x_{\nu}}\), we plug \(\boldsymbol{x_{\nu}}\) into the estimated regression equation:

\[\hat{\mu}_{\nu} = b_0 + b_1x_{\nu}.\]

To form the confidence interval, we appeal to our standard formula of \(\textbf{estimate} \boldsymbol{\mp t^*}\textbf{SE}_{\textbf{estimate}}\). The standard error for the estimated mean at any x-value, denoted \(\text{SE}_{\hat{\mu}_{\nu}}\), can be calculated as

\[\text{SE}_{\hat{\mu}_{\nu}} = \sqrt{\text{SE}^2_{b_1}(x_{\nu}-\bar{x})^2 + \frac{\hat{\sigma}^2}{n}}\]

where \(\hat{\sigma}^2\) is the squared residual standard error. This formula combines the variability in the slope estimate, \(\text{SE}_{b_1}\), scaled based on the distance of \(x_{\nu}\) from \(\bar{x}\) and the variability around the regression line, \(\hat{\sigma}^2\). Fortunately, R’s predict function can be used to provide these results for us and avoid doing this calculation by hand most of the time. The confidence interval for \(\boldsymbol{\mu_{\nu}}\), the population mean response at \(x_{\nu}\), is

\[\boldsymbol{\hat{\mu}_{\nu} \mp t^*_{n-2}}\textbf{SE}_{\boldsymbol{\hat{\mu}_{\nu}}}.\]

In application, these intervals get wider the further we go from the mean of the \(x\text{'s}\). These have interpretations that are exactly like those for the y-intercept:

For an x-value of \(\boldsymbol{x_{\nu}}\), we are __% confident that the true mean of y is between LL and UL [units of y].

It is also useful to remember that this interpretation applies individually to every \(x\) displayed in term-plots.

A second type of interval in this situation takes on a more challenging task – to place an interval on where we think a new observation will fall, called a prediction interval (PI). This PI will need to be much wider than the CI for the mean since we need to account for both the uncertainty in the mean and the randomness in sampling a new observation from the normal distribution centered at the true mean for \(x_{\nu}\). The interval is centered at the estimated regression line (where else could we center it?) with the estimate denoted as \(\hat{y}_{\nu}\) to help us see that this interval is for a new \(y\) at this x-value. The \(\text{SE}_{\hat{y}_{\nu}}\) incorporates the core of the previous SE calculation and adds in the variability of a new observation in \(\boldsymbol{\hat{\sigma}^2}\):

\[\text{SE}_{\hat{y}_{\nu}} = \sqrt{\text{SE}^2_{b_1}(x_{\nu}-\bar{x})^2 + \dfrac{\hat{\sigma}^2}{n} + \boldsymbol{\hat{\sigma}^2}} = \sqrt{\text{SE}_{\hat{\mu}_{\nu}}^2 + \boldsymbol{\hat{\sigma}^2}}\]

The __% PI is calculated as

\[\boldsymbol{\hat{y}_{\nu} \mp t^*_{n-2}}\textbf{SE}_{\boldsymbol{\hat{y}_{\nu}}}\]

and interpreted as:

We are __% sure that a new observation at \(\boldsymbol{x_{\nu}}\) will be between LL and UL [units of y]. Since \(\text{SE}_{\hat{y}_{\nu}} > \text{SE}_{\hat{\mu}_{\nu}}\), the PI will always be wider than the CI.

As in confidence intervals, we assume that a 95% PI “succeeds” – now when it succeeds it contains the new observation – in 95% of applications of the methods and fails the other 5% of the time. Remember that for any interval estimate, the true value is either in the interval or it is not and our confidence level essentially sets our failure rate! Because PIs push into the tails of the assumed distribution of the responses these methods are very sensitive to violations of assumptions so we should not use these if there are any concerns about violations of assumptions as they will work as advertised (at the nominal (specified) level).

There are two ways to explore CIs for the mean and PIs for a new observation. The first is to focus on a specific x-value of interest. The second is to plot the results for all \(x\text{'s}\). To do both of these, but especially to make plots, we want to learn to use the predict function. It can either produce the estimate for a particular \(x_{\nu}\) and the \(\text{SE}_{\hat{\mu}_{\nu}}\) or we can get it to directly calculate the CI and PI. The first way to use it is predict(MODELNAME, se.fit=T) which will provide fitted values and \(\text{SE}_{\hat{\mu}_{\nu}}\) for all observed \(x\text{'s}\). We can then use the \(\text{SE}_{\hat{\mu}_{\nu}}\) to calculate \(\text{SE}_{\hat{y}_{\nu}}\) and form our own PIs. If you want CIs, run predict(MODELNAME, interval= "confidence"); if you want PIs, run predict(MODELNAME, interval="prediction"). If you want to do prediction at an x-value that was not in the original observations, add the option newdata=tibble(XVARIABLENAME_FROM_ORIGINAL_MODEL=Xnu) to the predict function call.

Some examples of using the predict function follow¹¹¹. For example, it might be interesting to use the regression model to find a 95% CI and PI for the Beers vs BAC study for a student who would consume 8 beers. Four different applications of the predict function follow. Note that lwr and upr in the output depend on what we requested. The first use of predict just returns the estimated mean for 8 beers:

m1 <- lm(BAC~Beers, data=BB)
predict(m1, newdata=tibble(Beers=8))

##         1 
## 0.1310095

By turning on the se.fit=T option, we also get the SE for the confidence interval and degrees of freedom. Note that elements returned are labelled as $fit, $se.fit, etc. and provide some of the information to calculate CIs or PIs “by hand”.

predict(m1, newdata=tibble(Beers=8), se.fit=T)

## $fit
##         1 
## 0.1310095 
## 
## $se.fit
## [1] 0.009204354
## 
## $df
## [1] 14
## 
## $residual.scale
## [1] 0.02044095

Instead of using the components of the intervals to make them, we can also directly request the CI or PI using the interval=... option, as in the following two lines of code.

predict(m1, newdata=tibble(Beers=8), interval="confidence")

##         fit       lwr       upr
## 1 0.1310095 0.1112681 0.1507509

predict(m1, newdata=tibble(Beers=8), interval="prediction")

##         fit        lwr       upr
## 1 0.1310095 0.08292834 0.1790906

Based on these results, we are 95% confident that the true mean BAC for 8 beers consumed is between 0.111 and 0.15 grams of alcohol per dL of blood. For a new student drinking 8 beers, we are 95% sure that the observed BAC will be between 0.083 and 0.179 g/dL. You can see from these results that the PI is much wider than the CI – it has to capture a new individual’s results 95% of the time which is much harder than trying to capture the true mean at 8 beers consumed. For completeness, we should do these same calculations “by hand”. The predict(..., se.fit=T) output provides almost all the pieces we need to calculate the CI and PI. The $fit is the \(\text{estimate} = \hat{\mu}_{\nu}=0.131\), the $se.fit is the SE for the estimate of the \(\text{mean} = \text{SE}_{\hat{\mu}_{\nu}}=0.0092\) , $df is \(n-2 = 16-2=14\), and $residual.scale is \(\hat{\sigma}=0.02044\). So we just need the \(t^*\) multiplier for 95% confidence and 14 df:

qt(0.975, df=14) # t* multiplier for 95% CI or 95% PI

## [1] 2.144787

The 95% CI for the true mean at \(\boldsymbol{x_{\nu}=8}\) is then:

0.131 + c(-1,1)*2.1448*0.0092

## [1] 0.1112678 0.1507322

Which matches the previous output quite well.

The 95% PI requires the calculation of \(\sqrt{\text{SE}_{\hat{\mu}_{\nu}}^2 + \boldsymbol{\hat{\sigma}^2}} = \sqrt{(0.0092)^2+(0.02044)^2}=0.0224\).

sqrt(0.0092^2 + 0.02044^2)

## [1] 0.02241503

The 95% PI at \(\boldsymbol{x_{\nu}=8}\) is

0.131 + c(-1,1)*2.1448*0.0224

## [1] 0.08295648 0.17904352

These calculations are “fun” and informative but displaying these results for all x-values is a bit more informative about the performance of the two types of intervals and for results we might expect in this application. The calculations we just performed provide endpoints of both intervals at Beers= 8. To make this plot, we need to create a sequence of Beers values to get other results for, say from 0 to 10 beers, using the seq function. The seq function requires three arguments, that the endpoints (from and to) are defined and the length.out, which defines the resolution of the grid of equally spaced points to create. Here, length.out=30 provides 30 points evenly spaced between 0 and 10 and is more than enough to make the confidence and prediction intervals from 0 to 10 Beers.

beerf <- seq(from=0, to=10, length.out=30)
head(beerf,6)

## [1] 0.0000000 0.3448276 0.6896552 1.0344828 1.3793103 1.7241379

tail(beerf,6)

## [1]  8.275862  8.620690  8.965517  9.310345  9.655172 10.000000

Now we can call the predict function at the values stored in beerf to get the CIs across that range of Beers values:

BBCI <- as_tibble(predict(m1, newdata=tibble(Beers=beerf), interval="confidence"))
head(BBCI)

## # A tibble: 6 x 3
##         fit      lwr    upr
##       <dbl>    <dbl>  <dbl>
## 1 -0.0127   -0.0398  0.0144
## 2 -0.00651  -0.0320  0.0190
## 3 -0.000312 -0.0242  0.0236
## 4  0.00588  -0.0165  0.0282
## 5  0.0121   -0.00873 0.0329
## 6  0.0183   -0.00105 0.0376

And the PIs:

BBPI <- as_tibble(predict(m1, newdata=tibble(Beers=beerf), interval="prediction"))
head(BBPI)

## # A tibble: 6 x 3
##         fit     lwr    upr
##       <dbl>   <dbl>  <dbl>
## 1 -0.0127   -0.0642 0.0388
## 2 -0.00651  -0.0572 0.0442
## 3 -0.000312 -0.0502 0.0496
## 4  0.00588  -0.0433 0.0551
## 5  0.0121   -0.0365 0.0606
## 6  0.0183   -0.0296 0.0662

The rest of the code is just making a scatterplot and adding the five lines with a legend. The lines function connects the points with a line that provided and only works to add lines to the previously made plot. (lines()))

(ref:fig7-23) Estimated SLR for BAC data with 95% confidence (darker, dashed lines) and 95% prediction (lighter, dotted lines) intervals.

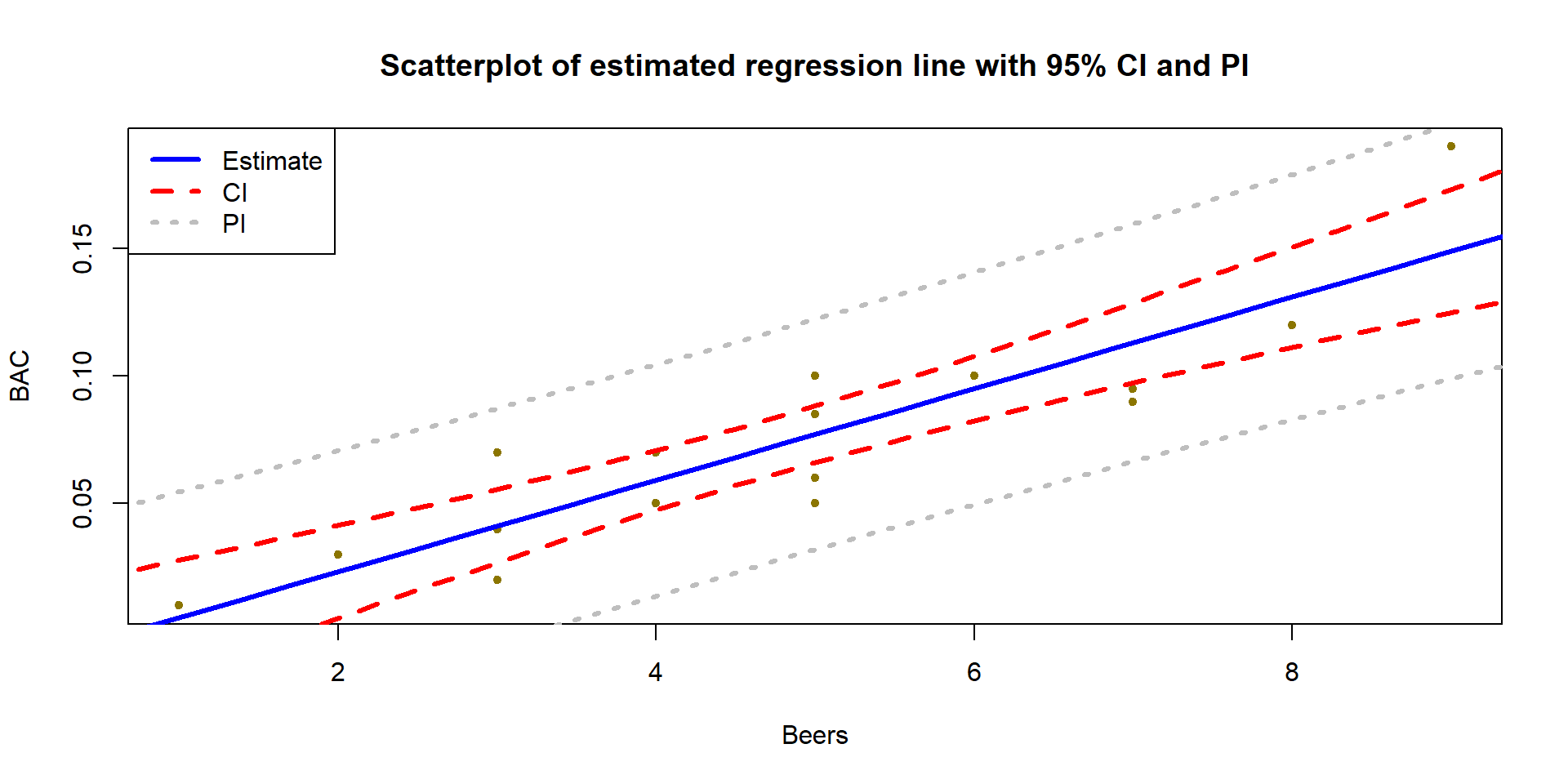
Figure 2.147: (ref:fig7-23)

par(mfrow=c(1,1))
plot(BAC~Beers, data=BB, xlab="Beers", ylab="BAC", pch=20, col="gold4",
     main="Scatterplot of estimated regression line with 95% CI and PI")
lines(fit~beerf, data=BBCI, col="blue", lwd=3) #Plot fitted values
lines(lwr~beerf, data=BBCI, col="red", lty=2, lwd=3) #Plot the CI lower bound
lines(upr~beerf, data=BBCI, col="red", lty=2, lwd=3) #Plot the CI upper bound
lines(lwr~beerf, data=BBPI, col="grey", lty=3, lwd=3) #Plot the PI lower bound
lines(upr~beerf, data=BBPI,col="grey", lty=3, lwd=3) #Plot the PI upper bound
legend("topleft", c("Estimate","CI","PI"), lwd=3, lty=c(1,2,3),
       col = c("blue","red","grey")) #Add a legend to explain lines

More importantly, note that the CI in Figure 2.147 clearly shows widening as we move further away from the mean of the \(x\text{'s}\) to the edges of the observed x-values. This reflects a decrease in knowledge of the true mean as we move away from the mean of the \(x\text{'s}\). The PI also is widening slightly but not as clearly in this situation. The difference in widths in the two types of intervals becomes extremely clear when they are displayed together, with the PI much wider than the CI for any \(x\)-value.

Similarly, the 95% CI and PIs for the Bozeman yearly average maximum temperatures in Figure 2.148 provide interesting information on the uncertainty in the estimated mean temperature over time. It is also interesting to explore how many of the observations fall within the 95% prediction intervals. The PIs are for new observations, but you can see how the PIs that were constructed to contain almost all the observations in the original data set but not all of them. In fact, only 2 of the 109 observations (1.8%) fall outside the 95% PIs. Since the PI needs to be concerned with unobserved new observations it makes sense that it might contain more than 95% of the observations used to make it.

(ref:fig7-24) Estimated SLR for Bozeman temperature data with 95% confidence (dashed lines) and 95% prediction (lighter, dotted lines) intervals.

temp1<-lm(meanmax~Year, data=bozemantemps)
 Yearf<-seq(from=1901,to=2014,length.out=75)
 
TCI<-as_tibble(predict(temp1,newdata= tibble(Year=Yearf),interval="confidence"))

TPI<-as_tibble(predict(temp1,newdata=tibble(Year=Yearf),interval="prediction"))

plot(meanmax~Year,data=bozemantemps,xlab="Year", ylab="degrees F",pch=20,col="darkgreen", main="Scatterplot of estimated regression line with 95% CI and PI")
 lines(fit~Yearf,data=TCI,col="blue",lwd=3)
 lines(lwr~Yearf,data=TCI,col="red",lty=2,lwd=3)
 lines(upr~Yearf,data=TCI,col="red",lty=2,lwd=3)
 lines(lwr~Yearf,data=TPI,col="grey",lty=3,lwd=3)
 lines(upr~Yearf,data=TPI,col="grey",lty=3,lwd=3)
legend("topleft", c("Estimate", "CI","PI"),lwd=3,lty=c(1,2,3),col = c("blue", "red","grey"))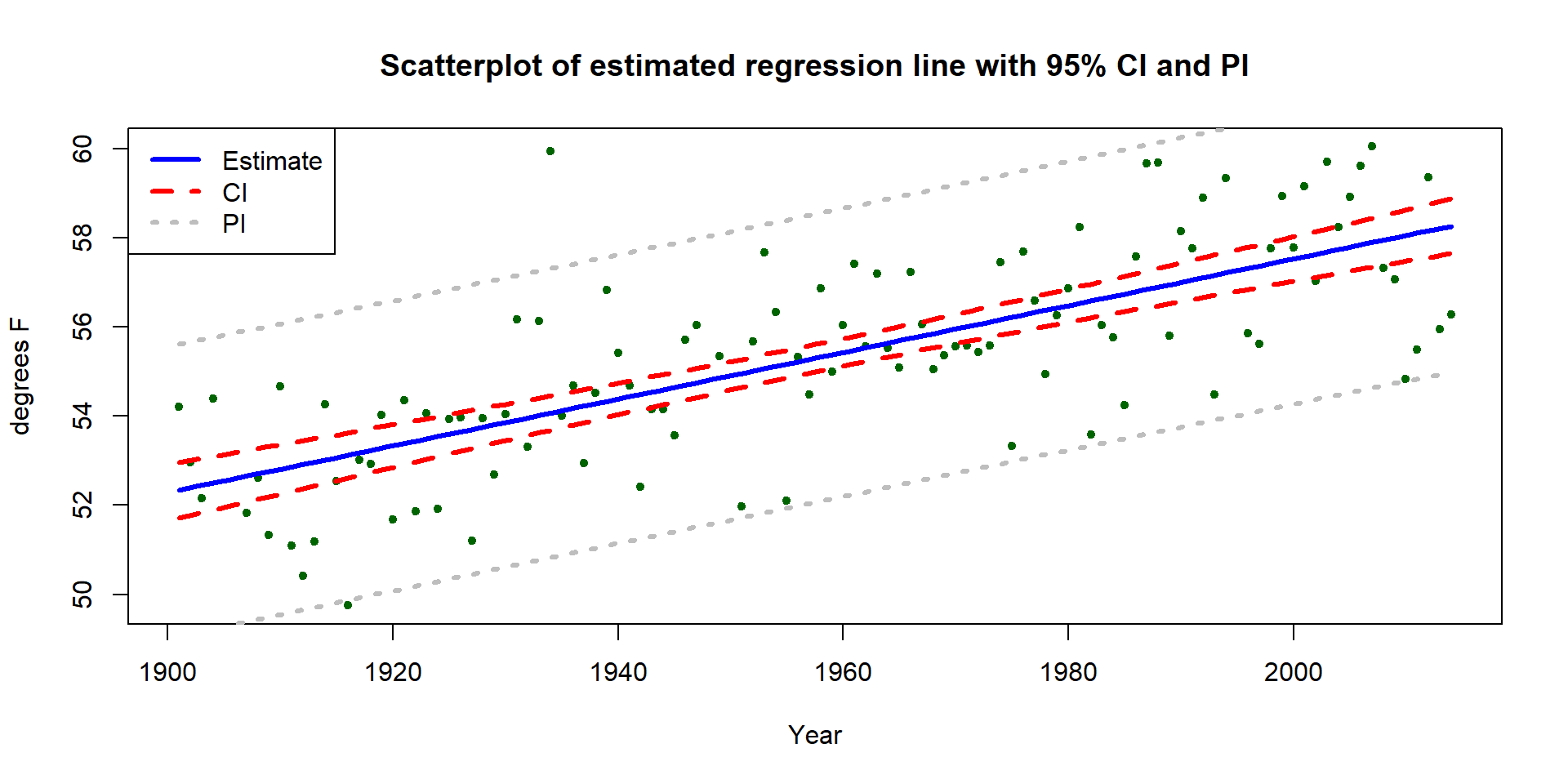

Figure 2.148: (ref:fig7-24)

We can also use these same methods to do a prediction for the year after the data set ended, 2015, and in 2050:

predict(temp1, newdata=tibble(Year=2015), interval="confidence")

##        fit     lwr      upr
## 1 58.31967 57.7019 58.93744

predict(temp1, newdata=tibble(Year=2015), interval="prediction")

##        fit      lwr      upr
## 1 58.31967 55.04146 61.59787

predict(temp1, newdata=tibble(Year=2050), interval="confidence")

##        fit      lwr      upr
## 1 60.15514 59.23631 61.07397

predict(temp1, newdata=tibble(Year=2050), interval="prediction")

##        fit      lwr      upr
## 1 60.15514 56.80712 63.50316

These results tell us that we are 95% confident that the true mean yearly average maximum temperature in 2015 is (I guess “was”) between 55.04\(^\circ F\) and 61.6\(^\circ F\). And we are 95% sure that the observed yearly average maximum temperature in 2015 will be (I guess “would have been”) between 59.2\(^\circ F\) and 61.1\(^\circ F\). Obviously, 2015 has occurred, but since the data were not published when the data set was downloaded in July 2016, we can probably best treat 2015 as a potential “future” observation. The results for 2050 are clearly for the future mean and a new observation¹¹² in 2050. Note that up to 2014, no values of this response had been observed above 60\(^\circ F\) and the predicted mean in 2050 is over 60\(^\circ F\) if the trend persists. It is easy to criticize the use of this model for 2050 because of its extreme amount of extrapolation.