- Cover
- Acknowledgments
- 1 Preface
- 2 (R)e-Introduction to statistics
- 2.1 Histograms, boxplots, and density curves
- 2.2 Pirate-plots
- 2.3 Models, hypotheses, and permutations for the two sample mean situation
- 2.4 Permutation testing for the two sample mean situation
- 2.5 Hypothesis testing (general)
- 2.6 Connecting randomization (nonparametric) and parametric tests
- 2.7 Second example of permutation tests
- 2.8 Reproducibility Crisis: Moving beyond p < 0.05, publication bias, and multiple testing issues
- 2.9 Confidence intervals and bootstrapping
- 2.10 Bootstrap confidence intervals for difference in GPAs
- 2.11 Chapter summary
- 2.12 Summary of important R code
- 2.13 Practice problems
- 3 One-Way ANOVA
- 3.1 Situation
- 3.2 Linear model for One-Way ANOVA (cell-means and reference-coding)
- 3.3 One-Way ANOVA Sums of Squares, Mean Squares, and F-test
- 3.4 ANOVA model diagnostics including QQ-plots
- 3.5 Guinea pig tooth growth One-Way ANOVA example
- 3.6 Multiple (pair-wise) comparisons using Tukey’s HSD and the compact letter display
- 3.7 Pair-wise comparisons for the Overtake data
- 3.8 Chapter summary
- 3.9 Summary of important R code
- 3.10 Practice problems
- 4 Two-Way ANOVA
- 4.1 Situation
- 4.2 Designing a two-way experiment and visualizing results
- 4.3 Two-Way ANOVA models and hypothesis tests
- 4.4 Guinea pig tooth growth analysis with Two-Way ANOVA
- 4.5 Observational study example: The Psychology of Debt
- 4.6 Pushing Two-Way ANOVA to the limit: Un-replicated designs and Estimability
- 4.7 Chapter summary
- 4.8 Summary of important R code
- 4.9 Practice problems
- 5 Chi-square tests
- 5.1 Situation, contingency tables, and tableplots
- 5.2 Homogeneity test hypotheses
- 5.3 Independence test hypotheses
- 5.4 Models for R by C tables
- 5.5 Permutation tests for the \(X^2\) statistic
- 5.6 Chi-square distribution for the \(X^2\) statistic
- 5.7 Examining residuals for the source of differences
- 5.8 General protocol for \(X^2\) tests
- 5.9 Political party and voting results: Complete analysis
- 5.10 Is cheating and lying related in students?
- 5.11 Analyzing a stratified random sample of California schools
- 5.12 Chapter summary
- 5.13 Summary of important R commands
- 5.14 Practice problems
- 6 Correlation and Simple Linear Regression
- 6.1 Relationships between two quantitative variables
- 6.2 Estimating the correlation coefficient
- 6.3 Relationships between variables by groups
- 6.4 Inference for the correlation coefficient
- 6.5 Are tree diameters related to tree heights?
- 6.6 Describing relationships with a regression model
- 6.7 Least Squares Estimation
- 6.8 Measuring the strength of regressions: R2
- 6.9 Outliers: leverage and influence
- 6.10 Residual diagnostics – setting the stage for inference
- 6.11 Old Faithful discharge and waiting times
- 6.12 Chapter summary
- 6.13 Summary of important R code
- 6.14 Practice problems
- 7 Simple linear regression inference
- 7.1 Model
- 7.2 Confidence interval and hypothesis tests for the slope and intercept
- 7.3 Bozeman temperature trend
- 7.4 Randomization-based inferences for the slope coefficient
- 7.5 Transformations part I: Linearizing relationships
- 7.6 Transformations part II: Impacts on SLR interpretations: log(y), log(x), & both log(y) & log(x)
- 7.7 Confidence interval for the mean and prediction intervals for a new observation
- 7.8 Chapter summary
- 7.9 Summary of important R code
- 7.10 Practice problems
- 8 Multiple linear regression
- 8.1 Going from SLR to MLR
- 8.2 Validity conditions in MLR
- 8.3 Interpretation of MLR terms
- 8.4 Comparing multiple regression models
- 8.5 General recommendations for MLR interpretations and VIFs
- 8.6 MLR inference: Parameter inferences using the t-distribution
- 8.7 Overall F-test in multiple linear regression
- 8.8 Case study: First year college GPA and SATs
- 8.9 Different intercepts for different groups: MLR with indicator variables
- 8.10 Additive MLR with more than two groups: Headache example
- 8.11 Different slopes and different intercepts
- 8.12 F-tests for MLR models with quantitative and categorical variables and interactions
- 8.13 AICs for model selection
- 8.14 Case study: Forced expiratory volume model selection using AICs
- 8.15 Chapter summary
- 8.16 Summary of important R code
- 8.17 Practice problems
- 9 Case studies
- 9.1 Overview of material covered
- 9.2 The impact of simulated chronic nitrogen deposition on the biomass and N2-fixation activity of two boreal feather moss–cyanobacteria associations
- 9.3 Ants learn to rely on more informative attributes during decision-making
- 9.4 Multi-variate models are essential for understanding vertebrate diversification in deep time
- 9.5 What do didgeridoos really do about sleepiness?
- 9.6 General summary
- References
5.2 Homogeneity test hypotheses
If we define some additional notation, we can then define hypotheses that allow us
to assess evidence related to whether the treatment “matters” in Homogeneity
situations.
This situation is similar to what we did in the One-Way ANOVA (Chapter ??)
situation with quantitative responses but the parameters now
relate to proportions in the response variable categories across the groups.
First we can define the conditional population proportions in level \(c\) (column
\(c=1,\ldots,C\)) of group \(r\) (row \(r=1,\ldots,R\)) as \(p_{rc}\).
Table 2.9 shows the proportions, noting that the proportions
in each row sum to 1 since they are conditional on the group of
interest. A transposed (rows and columns flipped) version of this table is
produced by the tally function if you use the formula ~y|x.
| Response Level 1 |
Response Level 2 |
Response Level 3 |
… |
Response Level C |
Totals |
|
|---|---|---|---|---|---|---|
| Group 1 | \(p_{11}\) | \(p_{12}\) | \(p_{13}\) | … | \(p_{1C}\) | \(\boldsymbol{1.0}\) |
| Group 2 | \(p_{21}\) | \(p_{22}\) | \(p_{23}\) | … | \(p_{2C}\) | \(\boldsymbol{1.0}\) |
| … | … | … | … | … | … | … |
| Group R | \(p_{R1}\) | \(p_{R2}\) | \(p_{R3}\) | … | \(p_{RC}\) | \(\boldsymbol{1.0}\) |
| Totals | \(\boldsymbol{p_{\bullet 1}}\) | \(\boldsymbol{n_{\bullet 2}}\) | \(\boldsymbol{p_{\bullet 3}}\) | … | \(\boldsymbol{p_{\bullet C}}\) | \(\boldsymbol{1.0}\) |
In the Homogeneity situation, the null hypothesis is that the distributions are the same in all the \(R\) populations. This means that the null hypothesis is:
\[\begin{array}{rl} \mathbf{H_0:}\ & \mathbf{p_{11}=p_{21}=\ldots=p_{R1}} \textbf{ and } \mathbf{p_{12}=p_{22}=\ldots=p_{R2}} \textbf{ and } \mathbf{p_{13}=p_{23}=\ldots=p_{R3}} \\ & \textbf{ and } \mathbf{\ldots} \textbf{ and }\mathbf{p_{1C}=p_{2C}=\ldots=p_{RC}}. \\ \end{array}\]
If all the groups are the same, then they all have the same conditional proportions and we can more simply write the null hypothesis as:
\[\mathbf{H_0:(p_{r1},p_{r2},\ldots,p_{rC})=(p_1,p_2,\ldots,p_C)} \textbf{ for all } \mathbf{r}.\]
In other words, the pattern of proportions across the columns are the same for all the \(\mathbf{R}\) groups. The alternative is that there is some difference in the proportions of at least one response category for at least one group. In slightly more gentle and easier to reproduce words, equivalently, we can say:
- \(\mathbf{H_0:}\) The population distributions of the responses for variable \(\mathbf{y}\) are the same across the \(\mathbf{R}\) groups.
The alternative hypothesis is then:
- \(\mathbf{H_A:}\) The population distributions of the responses for variable \(\mathbf{y}\) are NOT ALL the same across the \(\mathbf{R}\) groups.
To make this concrete, consider what the proportions could look like if they satisfied the null hypothesis for the Arthritis example, as displayed in Figure 2.75.
(ref:fig5-4) Plot of one way that the Arthritis proportions could have been if the null hypothesis had been true.
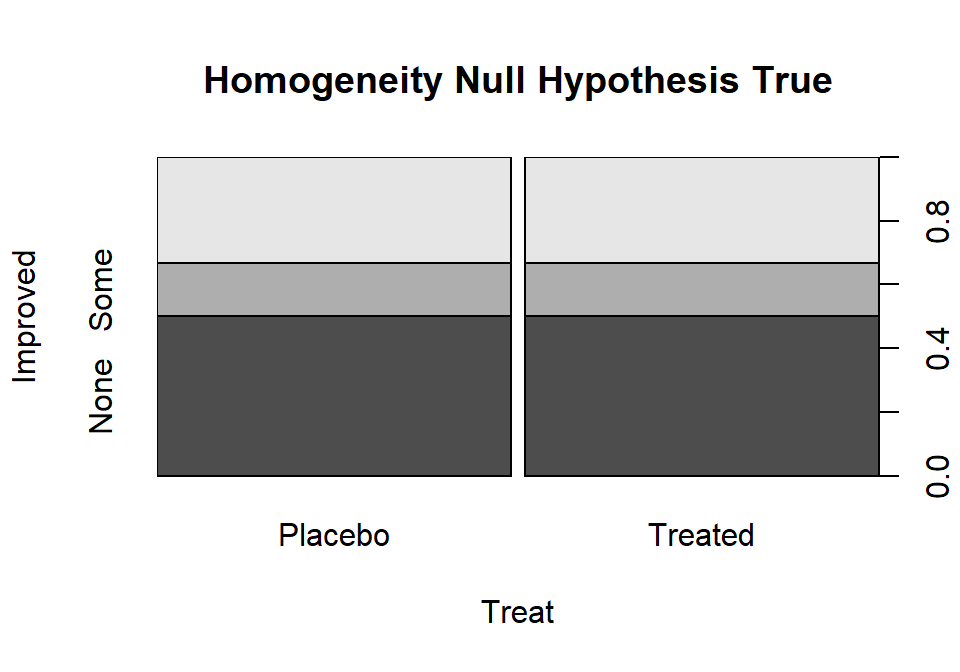
Figure 2.75: (ref:fig5-4)
Note that the proportions in the different response categories do not need to be the same just that the distribution needs to be the same across the groups. The null hypothesis does not require that all three response categories (none, some, marked) be equally likely. It assumes that whatever the distribution of proportions is across these three levels of the response that there is no difference in that distribution between the explanatory variable (here treated/placebo) groups. Figure 2.75 shows an example of a situation where the null hypothesis is true and the distributions of responses across the groups look the same but the proportions for none, some and marked are not all equally likely. That situation satisfies the null hypothesis. Compare this plot to the one for the real data set in Figure 2.73. It looks like there might be some differences in the responses between the treated and placebo groups as that plot looks much different from this one, but we will need a test statistic and a p-value to fully address the evidence relative to the previous null hypothesis.