5.7 Examining residuals for the source of differences

Small p-values are generated by large \(X^2\) values. If we want to understand the source of a small p-value, we need to understand what made the test statistic large. To get a large \(X^2\) value, we either need many small contributions from lots of cells or a few large contributions. In most situations, there are just a few cells that show large deviations between the null hypothesis (expected cell counts) and what was observed (observed cell counts). It is possible to explore the “size” and direction of the differences between observed and expected counts to learn something about the behavior of the relationship between the variables, especially as it relates to evidence against the null hypothesis of no difference or no relationship. The standardized residual,

\[\boldsymbol{\left(\frac{\textbf{Observed}_i - \textbf{Expected}_i}{\sqrt{\textbf{Expected}_i}}\right)},\]

provides a measure of deviation of the observed from expected which retains the direction of deviation (whether observed was more or less than expected is interesting for interpretations) for each cell in the table. It is scaled much like a standard normal distribution providing a scale for “large” deviations for absolute values that are over 2 or 3. In other words, values with magnitude over 2 should be your focus in the standardized residuals, noting whether the observed counts were much more or less than expected. On the \(X^2\) scale, standardized residuals of 2 or more mean that the cells are contributing 4 or more units to the overall statistic, which is a pretty noticeable bump up in the size of the statistic. A few contributions at 4 or higher and you will likely end up with a small p-value.

There are two ways to explore standardized residuals. First, we can obtain them via the chisq.test and manually identify the “big ones”. Second, we can augment a mosaic plot of the table with the standardized results by turning on the shade=T option and have the plot help us find the big differences. This technique can be applied whether we are performing an Independence or Homogeneity test – both are evaluated with the same \(X^2\) statistic so the large standardized residuals are of interest in both situations. Both types of results are shown for the Arthritis data table:

(ref:fig5-12) Mosaic plot of the Arthritis data with large standardized residuals indicated (actually, there were none that were indicated because all were less than 2). Note that dashed borders correspond to negative standardized residuals (observed less than expected) and solid borders are positive standardized residuals (observed more than expected).

##          Improved
## Treatment        None        Some      Marked
##   Placebo  1.61749160 -0.06225728 -1.93699199
##   Treated -1.65647289  0.06375767  1.98367320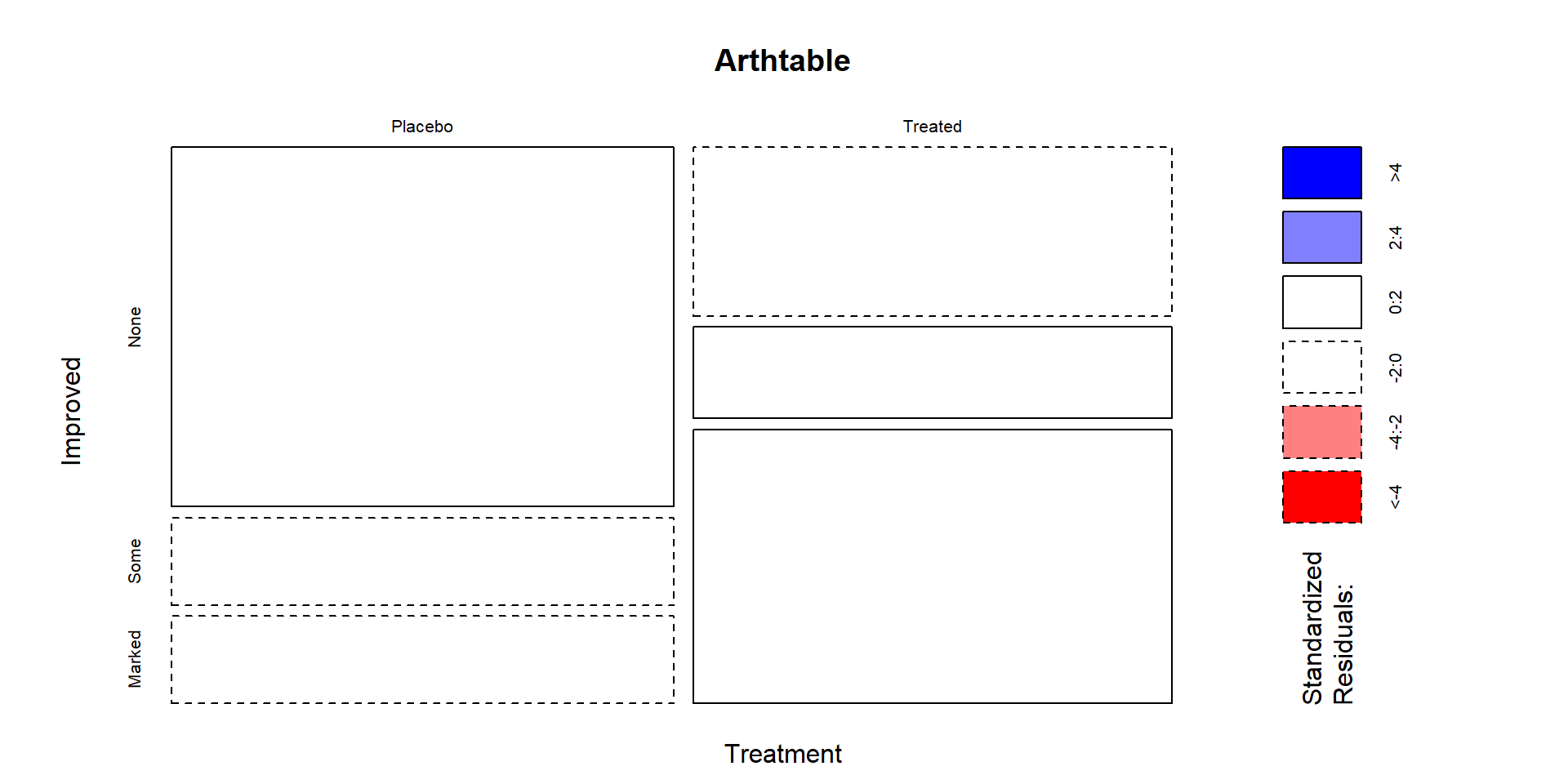
(ref:fig5-12)

Figure 2.83: (ref:fig5-12)

In these data, the standardized residuals are all less than 2 in magnitude so Figure 2.83 isn’t too helpful but this type of plot is in other examples. The largest contributions to the \(X^2\) statistic come from the Placebo and Treated groups in the Marked improvement cells. Those standardized residuals are -1.94 and 1.98 (both really close to 2), showing that the placebo group had noticeably fewer Marked improvement
results than expected and the Treated group had noticeably more Marked improvement responses than expected if the null hypothesis was true. Similarly but with smaller magnitudes, there were more None results than expected in the Placebo group and fewer None results than expected in the Treated group. The standardized residuals were very small in the two cells for the Some improvement category, showing that the treatment/placebo were similar in this response category and that the results were about what would be expected if the null hypothesis of no difference were true.