8.13 AICs for model selection

There are a variety of techniques for selecting among a set of potential models or refining an initially fit MLR model. Hypothesis testing can be used (in the case where we have nested models either by adding or deleting a single term at a time) or comparisons of adjusted R² across different potential models (which is valid for nested or non-nested model comparisons). Diagnostics should play a role in the models considered and in selecting among models that might appear to be similar on a model comparison criterion. In this section, a new model selection method is introduced that has stronger theoretical underpinnings, a slightly more interpretable scale, and, often, better performance in picking an optimal¹³⁶ model than the adjusted R². The measure is called the AIC (Akaike’s An Information Criterion¹³⁷, (Akaike 1974). It is extremely popular, but sometimes misused, in some fields such as Ecology and has been applied in almost every other potential application area where statistical models can be compared. Burnham and Anderson (2002) have been responsible for popularizing the use of AIC for model selection, especially in Ecology. The AIC is an estimate of the distance (or discrepancy or divergence) between a candidate model and the true model, on a log-scale, based on a measure called the Kullback-Leibler divergence. The models that are closer (have a smaller distance) to the truth are better and we can compare how close two models are to the truth, picking the one that has a smaller distance (smaller AIC) as better. The AIC includes a component that is on the log-scale, so negative values are possible and you should not be disturbed if you are comparing large magnitude negative numbers – just pick the model with the smallest AIC score.

The AIC is optimized (smallest) for a model that contains the optimal balance of simplicity of the model with quality of fit to the observations. Scientists are driven to different degrees by what is called the principle of parsimony: that simpler explanations (models) are better if everything else is equal or even close to equal. In this case, it would mean that if two models are similarly good on AIC, then select the simpler of the two models since it is more likely to be correct in general than the more complicated model. The AIC is calculated as \(AIC=-2log(Likelihood)+2m\), where the Likelihood provides a measure of fit of the model (we let R calculate it for us) and gets smaller for better fitting models and \(m\) = (number of estimated \(\beta\text{'s}+1\)). The value \(m\) is called the model degrees of freedom for AIC calculations and relates to how many total parameters are estimated. Note that it is a different measure of degrees of freedom than used in ANOVA \(F\)-tests. The main things to understand about the formula for the AIC is that as \(m\) increases, the AIC will go up and that as the fit improves, the likelihood will increase (so -2log-likelihood will get smaller)¹³⁸.

There are some facets of this discussion to keep in mind when comparing models. More complicated models always fit better (we saw this for the R² measure, as the proportion of variation explained always goes up if more “stuff” is put into the model even if the “stuff” isn’t useful). The AIC resembles the adjusted R² in that it incorporates the count of the number of parameters estimated. This allows the AIC to make sure that enough extra variability is explained in the responses to justify making the model more complicated (increasing \(m\)). The optimal model on AIC has to balance adding complexity and increasing quality of the fit. Since this measure provides an estimate of the distance or discrepancy to the “true model”, the model with the smallest value “wins” – it is top-ranked on the AIC. Note that the top-ranked AIC model will often not be the best fitting model since the best fitting model is always the most complicated model considered. The top AIC model is the one that is estimated to be closest to the truth, where the truth is still unknown…

To help with interpreting the scale of AICs, they are often reported in a table sorted from smallest to largest values with the AIC and the “delta AIC” or, simply, \(\Delta\text{AIC}\) reported. The

\[\Delta\text{AIC}=\text{AIC}_{\text{model}} - \text{AIC}_{\text{topModel}}\]

and so provides a value of 0 for the top-ranked AIC model and a measure of how much worse on the AIC scale the other models are. A rule of thumb is that a 2 unit difference on AICs \((\Delta\text{AIC}=2)\) is decent evidence of a difference in the models and more than 4 units \((\Delta\text{AIC}>4)\) is a really big difference. This is more based on experience than a distinct reason or theoretical result but seems to provide reasonable results in most situations. Often researchers will consider any models within 2 AIC units of the top model \((\Delta\text{AIC}<2)\) as indistinguishable on AICs and so either select the simplest model of the choices or report all the models with similar “support”, allowing the reader to explore the suite of similarly supported potential models . It is important to remember that if you search across too many models, even with the AIC to support your model comparisons, you might find a spuriously top model. Individual results that are found by exploring many tests or models have higher chances to be spurious and results found in this manner are difficult to reproduce when someone repeats a similar study¹³⁹. For these reasons, there is a set of general recommendations that have been developed for using AICs:

• Consider a suite of models (often pre-specified and based on prior research in the area of interest) and find the models with the top (in other words, smallest) AIC results.

  • The suite of candidate models need to contain at least some good models. Selecting the best of a set of BAD models only puts you at the top of $%#%-mountain, which is not necessarily a good thing.

• Report a table with the models considered, sorted from smallest to largest AICs (\(\Delta\text{AICs}\) from smaller to larger) that includes a count of number of parameters estimated¹⁴⁰, the AICs, and \(\Delta\text{AICs}\).

  • Remember to incorporate the mean-only model in the model selection results. This allows you to compare the top model to one that does not contain any predictors.

• Interpret the top model or top models if a few are close on the AIC-scale to the top model.

• DO NOT REPORT P-VALUES OR CALL TERMS “SIGNIFICANT” when models were selected using AICs.

  • Hypothesis testing and AIC model selection are not compatible philosophies and testing in models selected by AICs invalidates the tests as they have inflated Type I error rates. The AIC results are your “evidence” – you don’t need anything else. If you wanted to report p-values, use them to select your model.

• You can describe variables as “important” or “useful” and report confidence intervals to aid in interpretation of the terms in the selected model(s) but need to avoid performing hypothesis tests with the confidence intervals.

• Remember that the selected model is not the “true” model – it is only the best model according to AIC among the set of models you provided.

• Model assumptions need to be met to use AICs. They assume that the model is specified correctly up to possibly comparing different predictor variables. Perform diagnostic checks on your initial model and the top model.

When working with AICs, there are two options. Fit the models of interest and then run the AIC function on each model. This can be tedious, especially when we have many possible models to consider. We can make it easy to fit all the potential candidate models that are implied by a complicated starting model by using the dredge function from the MuMIn package (Barton 2019). The name (dredge) actually speaks to what fitting all possible models really engages – what is called data dredging. The term is meant to refer to considering way too many models for your data set, probably finding something good from the process, but maybe identifying something spurious since you looked at so many models. Note that if you take a hypothesis testing approach where you plan to remove any terms with large p-values in this same situation, you are really considering all possible models as well because you could have removed some or all model components. Methods that consider all possible models are probably best used in exploratory analyses where you do not know if any or all terms should be important. If you have more specific research questions, then you probably should try to focus on comparisons of models that help you directly answer those questions, either with AIC or p-value methods.

The dredge function provides an automated method of assessing all possible simpler models based on an initial (full) model. It generates a table of AIC results, \(\Delta\text{AICs}\), and also shows when various predictors are in or out of the model for all reduced models possible from an initial model. For quantitative predictors, the estimated slope is reported when that predictor is in the model. For categorical variables and interactions with them, it just puts a “+” in the table to let you know that the term is in the models. Note that you must run the options(na.action = "na.fail") code to get dredge to work.

To explore the AICs and compare their results to the adjusted R² that we used before for model selection, we can revisit the Snow Depth data set with related results found in Section 8.4 and Table 2.13. In that situation we were considering a “full” model that included Elevation, Min.Temp, and Max.Temp as potential predictor variables after removing two influential points. And we considered all possible reduced models from that “full”¹⁴¹ model. Note that the dredge output adds one more model that adjusted R² can’t consider – the mean-only model that contains no predictor variables. In the following output it is the last model in the output (worst ranked on AIC). Including the mean-only model in these results helps us “prove” that there is support for having something in the model, but only if there is better support for other models than this simplest possible model.

In reading dredge output¹⁴² as it is constructed here, the models are sorted by top to bottom AIC values (smallest AIC to largest). The column delta is for the \(\Delta\text{AICs}\) and shows a 0 for the first row, which is the top-ranked AIC model. Here it is for the model with Elevation and Max.Temp but not including Min.Temp. This was also the top ranked model from adjusted R², which is reproduced in the adjRsq column. The AIC is calculated using the previous formula based on the df and logLik columns. The df is also a useful column for comparing models as it helps you see how complex each model is. For example, the top model used up 4 model df (three \(\beta\text{'s}\) and the residual error variance) and the most complex model that included four predictor variables used up 5 model df.

library(MuMIn)
options(na.action = "na.fail") #Must run this code once to use dredge
snotel2R<-snotel2[-c(9,22),]; m6 <- lm(Snow.Depth~Elevation+Min.Temp+Max.Temp, data=snotel2R)
dredge(m6, rank="AIC",
       extra = c("R^2", adjRsq=function(x) summary(x)$adj.r.squared))

## Global model call: lm(formula = Snow.Depth ~ Elevation + Min.Temp + Max.Temp, data = snotel2R)
## ---
## Model selection table 
##     (Int)     Elv Max.Tmp Min.Tmp    R^2 adjRsq df   logLik   AIC delta
## 4 -167.50 0.02408  1.2530         0.8495 0.8344  4  -80.855 169.7  0.00
## 8 -213.30 0.02686  1.2430  0.9843 0.8535 0.8304  5  -80.541 171.1  1.37
## 2  -80.41 0.01791                 0.8087 0.7996  3  -83.611 173.2  3.51
## 6 -130.70 0.02098          1.0660 0.8134 0.7948  4  -83.322 174.6  4.93
## 5  179.60                 -5.0090 0.6283 0.6106  3  -91.249 188.5 18.79
## 7  178.60         -0.2687 -4.6240 0.6308 0.5939  4  -91.170 190.3 20.63
## 3  119.50         -2.1800         0.4131 0.3852  3  -96.500 199.0 29.29
## 1   40.21                         0.0000 0.0000  2 -102.630 209.3 39.55
##   weight
## 4  0.568
## 8  0.286
## 2  0.098
## 6  0.048
## 5  0.000
## 7  0.000
## 3  0.000
## 1  0.000
## Models ranked by AIC(x)

You can use the table of results from dredge to find information to compare the estimated models. There are two models that are clearly favored over the others with \(\Delta\text{AICs}\) for the model with Elevation and Max.Temp of 0 and for the model with all three predictors of 1.37. The \(\Delta\text{AIC}\) for the third ranked model (contains just Elevation) is 3.51 suggesting clear support for the top model over this because of a difference of 3.51 AIC units to the truth. The difference between the second and third ranked models also provides relatively strong support for the more complex model over the model with just Elevation. And the mean-only model had a \(\Delta\text{AIC}\) of nearly 40 – suggesting extremely strong evidence for the top model versus using no predictors. So we have pretty clear support for models that include the Elevation and Max.Temp variables (in both top models) and some support for also including the Min.Temp, but the top model did not require its inclusion. It is also possible to think about the AICs as a result on a number line from “closest to the truth” to “farthest” for the suite of models considered, as shown in Figure 2.186.

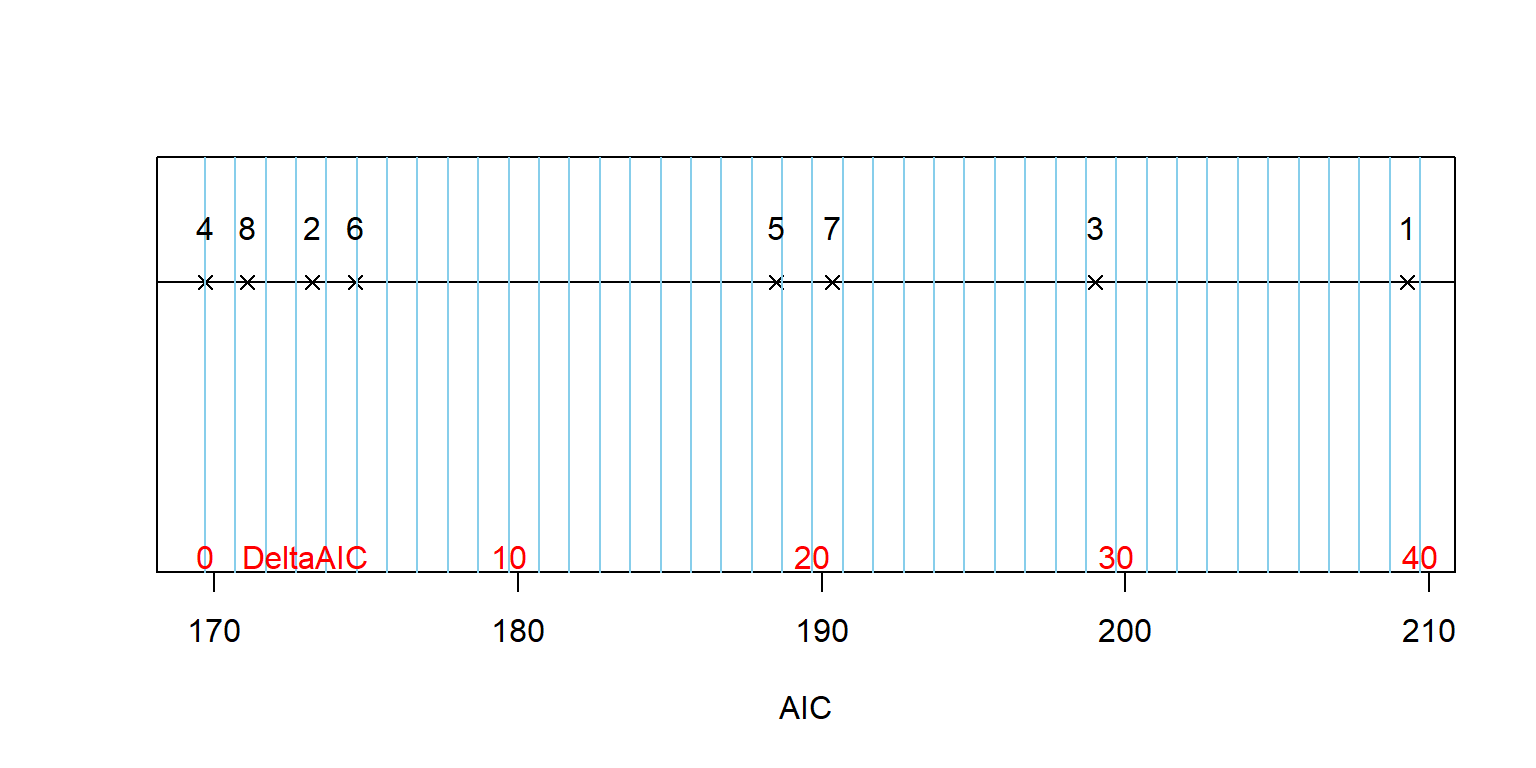
Figure 2.186: Display of AIC results on a number line with models indicated by their number in the dredge output. Note that the actual truth is unknown but further left in the plot corresponds to the models that are estimated to be closer to the truth and so there is stronger evidence for those models versus the others.

We could add further explorations of the term-plots and confidence intervals for the slopes from the top or, here, possibly top two models. We would not spend any time with p-values since we already used the AIC to assess evidence related to the model components and they are invalid if we model select prior to reporting them. We can quickly compare the slopes for variables that are shared in the two models since they are both quantitative variables using the output. It is interesting that the Elevation and Max.Temp slopes change little with the inclusion of Min.Temp in moving from the top to second ranked model (0.02408 to 0.0286 and 1.253 to 1.243).

This was an observational study and so we can’t consider causal inferences here as discussed previously. Generally, the use of AICs does not preclude making causal statements but if you have randomized assignment of levels of an explanatory variable, it is more philosophically consistent to use hypothesis testing methods in that setting. If you went to the effort to impose the levels of a treatment on the subjects, it also makes sense to see if the differences created are beyond what you might expect by chance if the treatment didn’t matter.