6.8 Measuring the strength of regressions: R2

At the beginning of the chapter, we used the correlation coefficient to measure the strength and direction of the linear relationship. The regression line provides an even more detailed description of the direction of the linear relationship than the correlation provided; in regression we addressed the question of “for a unit change in \(x\), what sort of change in \(y\) do we expect, on average?” whereas the correlation just addressed whether the relationship was positive or negative. However, the regression line tells us nothing about the strength of the relationship. Consider the three scatterplots in Figure 2.118: the left panel is the original BAC data and the two right panels have fake data that generated exactly the same estimated regression model with a weaker (middle panel) and then a stronger (right panel) linear relationship between Beers and BAC. This suggests that the regression line is a useful but incomplete characterization of relationships between variables – we need a measure of strength of the relationship to go with the equation.

We could use the correlation coefficient, r, again to characterize strength but it is somewhat redundant to report a measure that contains direction information. It also will not extend to multiple regression models where we have more than one predictor variable in the same model.

In regression models, we use the coefficient of determination (symbol: R2) to accompany our regression line and describe the strength of the relationship. It can either be scaled between 0 and 1 or 0 to 100% and has “units” of the proportion or percentage of the variation in \(y\) that is explained by the model that includes \(x\) (and later more than one \(x\)). For example, an R2 of 0% corresponds to explaining 0% of the variation in the response with our model and \(\boldsymbol{R^2} = 100\%\) means that all the variation in the response was explained by the model. In between, it provides a nice summary of how much of the total variability in the response we can account for with our model including \(x\) (and, in Chapter ??, including multiple predictor variables).

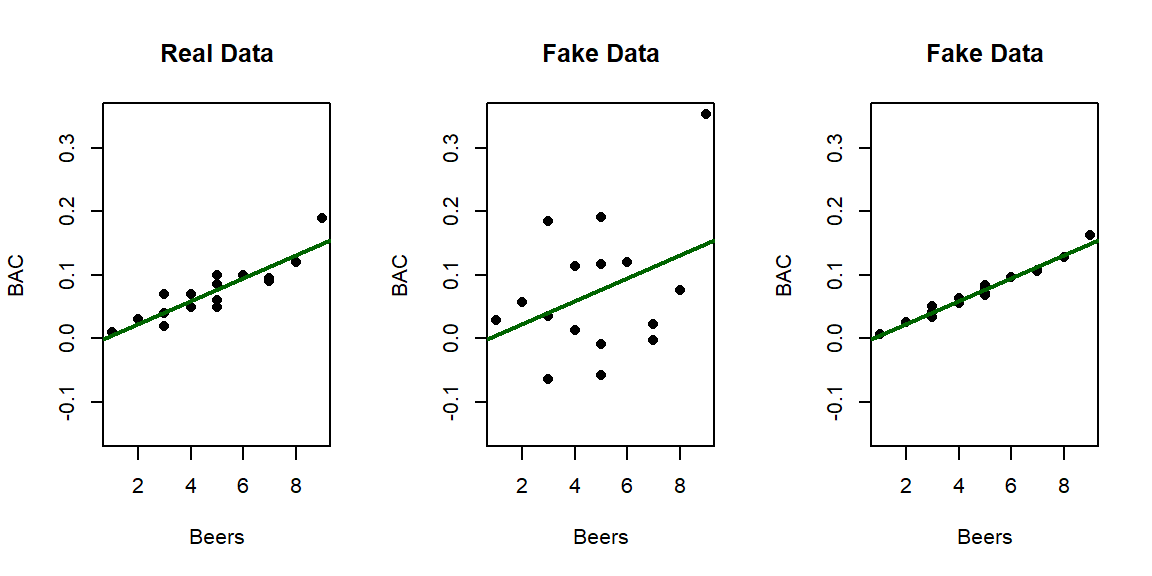
Three scatterplots with the same estimated regression line.

Figure 2.118: Three scatterplots with the same estimated regression line.

The R2 is calculated using the sums of squares we encountered in the ANOVA methods. We once again have some total amount of variability that is attributed to the variation based on the model fit, here we call it \(\text{SS}_\text{regression}\), and the residual variability, still \(\text{SS}_\text{error}=\Sigma(y-\hat{y})^2\). The \(\text{SS}_\text{regression}\) is most easily calculated as \(\text{SS}_\text{regression} = \text{SS}_\text{Total} - \text{SS}_\text{error}\), the difference between the total variability and the variability not explained by the model under consideration. Using these quantities, we calculate the portion of the total variability that the model explains as

\[\boldsymbol{R^2}=\frac{\text{SS}_\text{regression}}{\text{SS}_\text{Total}} =1 - \frac{\text{SS}_\text{error}}{\text{SS}_\text{Total}}.\]

It also ends up that the coefficient of determination for models with one predictor is the correlation coefficient (r) squared (\(\boldsymbol{R^2} = \boldsymbol{r^2}\)). So we can quickly find coefficients of determination if we know correlations in simple linear regression models. In the real Beers and BAC data, r=0.8943. So \(\boldsymbol{R^2} = 0.79998\) or approximately 0.80. So 80% of the variation in BAC is explained by Beer consumption. That leaves 20% of the variation in the responses to be unexplained by our model. In this case much of the unexplained variation is likely attributable to differences in physical characteristics (that were not measured) but the statistical model places that unexplained variation into the category of “random errors”. We don’t actually have to find r to get coefficients of determination – the result is part of the regular summary of a regression model that we have not discussed. We repeat the full lm model summary below – note that a number is reported for the “Multiple R-squared” in the second to last line of the output. It is reported as a proportion and it is your choice whether you want to report and interpret it as a proportion or percentage, just make that clear in how you discuss it.

## 
## Call:
## lm(formula = BAC ~ Beers, data = BB)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.027118 -0.017350  0.001773  0.008623  0.041027 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.012701   0.012638  -1.005    0.332
## Beers        0.017964   0.002402   7.480 2.97e-06
## 
## Residual standard error: 0.02044 on 14 degrees of freedom
## Multiple R-squared:  0.7998, Adjusted R-squared:  0.7855 
## F-statistic: 55.94 on 1 and 14 DF,  p-value: 2.969e-06

In this output, be careful because there is another related quantity called Adjusted R-squared that we will discuss later. This other quantity is not a measure of the strength of the relationship but will be useful.

We could also revisit the ANOVA table for this model to verify the source of the R2 of 0.80 based on \(\text{SS}_\text{regression}= 0.02337\) and \(\text{SS}_\text{Total} = 0.02337+0.00585\). This provides 0.80 from \(0.02337/0.02922\).

## Analysis of Variance Table
## 
## Response: BAC
##           Df    Sum Sq   Mean Sq F value    Pr(>F)
## Beers      1 0.0233753 0.0233753  55.944 2.969e-06
## Residuals 14 0.0058497 0.0004178
## [1] 0.7998392

In Figure 2.118, there are three examples with the same regression model, but different strengths of relationships. In the real data set \(\boldsymbol{R^2} = 80\%\). For the first fake data set (middle panel), the R2 drops to \(13.8\%\) and for the second fake data set (right panel), R2 is \(97.3\%\). As a summary, R2 provides a natural scale to understand “how good” each model is at explaining the responses. We can revisit some of our previous models to get a little more practice with using this summary of strength or quality of regression models.

For the Montana fire data, \(\boldsymbol{R^2}=66.2\%\). So the proportion of variation of log-area burned that is explained by average summer temperature is 0.662. This is “good” but also leaves quite a bit of unexplained variation in the responses. There is a long list of reasons why this explanatory variable leaves a lot of variation in the response unexplained. Note that we were careful about using the scaling of the response variable (log(area burned)) in the interpretation – this is because we would get a much different answer if area burned vs temperature was considered.

## 
## Call:
## lm(formula = loghectares ~ Temperature, data = mtfires)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.0822 -0.9549  0.1210  1.0007  2.4728 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) -69.7845    12.3132  -5.667 1.26e-05
## Temperature   1.3884     0.2165   6.412 2.35e-06
## 
## Residual standard error: 1.476 on 21 degrees of freedom
## Multiple R-squared:  0.6619, Adjusted R-squared:  0.6458 
## F-statistic: 41.12 on 1 and 21 DF,  p-value: 2.347e-06

For the model for female Australian athletes that used Body fat to explain Hematocrit, the estimated regression model was \(\widehat{\text{Hc}}_i = 42.014 - 0.085\cdot\text{BodyFat}_i\) and \(\boldsymbol{r} = -0.168\). The coefficient of determination is \(\boldsymbol{R^2} = (-0.168)^2 = 0.0282\). So body fat explains 2.8% of the variation in Hematocrit in these women. That is not a very good regression model with over 97% of the variation in Hematocrit unexplained by this model. The scatterplot showed a fairly weak relationship but this provides numerical and interpretable information that drives that point home.

## 
## Call:
## lm(formula = Hc ~ Bfat, data = subset(aisR2, Sex == 1))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.2399 -2.2132 -0.1061  1.8917  6.6453 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) 42.01378    0.93269  45.046   <2e-16
## Bfat        -0.08504    0.05067  -1.678   0.0965
## 
## Residual standard error: 2.598 on 97 degrees of freedom
## Multiple R-squared:  0.02822,    Adjusted R-squared:  0.0182 
## F-statistic: 2.816 on 1 and 97 DF,  p-value: 0.09653