- Cover
- Acknowledgments
- 1 Preface
- 2 (R)e-Introduction to statistics
- 2.1 Histograms, boxplots, and density curves
- 2.2 Pirate-plots
- 2.3 Models, hypotheses, and permutations for the two sample mean situation
- 2.4 Permutation testing for the two sample mean situation
- 2.5 Hypothesis testing (general)
- 2.6 Connecting randomization (nonparametric) and parametric tests
- 2.7 Second example of permutation tests
- 2.8 Reproducibility Crisis: Moving beyond p < 0.05, publication bias, and multiple testing issues
- 2.9 Confidence intervals and bootstrapping
- 2.10 Bootstrap confidence intervals for difference in GPAs
- 2.11 Chapter summary
- 2.12 Summary of important R code
- 2.13 Practice problems
- 3 One-Way ANOVA
- 3.1 Situation
- 3.2 Linear model for One-Way ANOVA (cell-means and reference-coding)
- 3.3 One-Way ANOVA Sums of Squares, Mean Squares, and F-test
- 3.4 ANOVA model diagnostics including QQ-plots
- 3.5 Guinea pig tooth growth One-Way ANOVA example
- 3.6 Multiple (pair-wise) comparisons using Tukey’s HSD and the compact letter display
- 3.7 Pair-wise comparisons for the Overtake data
- 3.8 Chapter summary
- 3.9 Summary of important R code
- 3.10 Practice problems
- 4 Two-Way ANOVA
- 4.1 Situation
- 4.2 Designing a two-way experiment and visualizing results
- 4.3 Two-Way ANOVA models and hypothesis tests
- 4.4 Guinea pig tooth growth analysis with Two-Way ANOVA
- 4.5 Observational study example: The Psychology of Debt
- 4.6 Pushing Two-Way ANOVA to the limit: Un-replicated designs and Estimability
- 4.7 Chapter summary
- 4.8 Summary of important R code
- 4.9 Practice problems
- 5 Chi-square tests
- 5.1 Situation, contingency tables, and tableplots
- 5.2 Homogeneity test hypotheses
- 5.3 Independence test hypotheses
- 5.4 Models for R by C tables
- 5.5 Permutation tests for the \(X^2\) statistic
- 5.6 Chi-square distribution for the \(X^2\) statistic
- 5.7 Examining residuals for the source of differences
- 5.8 General protocol for \(X^2\) tests
- 5.9 Political party and voting results: Complete analysis
- 5.10 Is cheating and lying related in students?
- 5.11 Analyzing a stratified random sample of California schools
- 5.12 Chapter summary
- 5.13 Summary of important R commands
- 5.14 Practice problems
- 6 Correlation and Simple Linear Regression
- 6.1 Relationships between two quantitative variables
- 6.2 Estimating the correlation coefficient
- 6.3 Relationships between variables by groups
- 6.4 Inference for the correlation coefficient
- 6.5 Are tree diameters related to tree heights?
- 6.6 Describing relationships with a regression model
- 6.7 Least Squares Estimation
- 6.8 Measuring the strength of regressions: R2
- 6.9 Outliers: leverage and influence
- 6.10 Residual diagnostics – setting the stage for inference
- 6.11 Old Faithful discharge and waiting times
- 6.12 Chapter summary
- 6.13 Summary of important R code
- 6.14 Practice problems
- 7 Simple linear regression inference
- 7.1 Model
- 7.2 Confidence interval and hypothesis tests for the slope and intercept
- 7.3 Bozeman temperature trend
- 7.4 Randomization-based inferences for the slope coefficient
- 7.5 Transformations part I: Linearizing relationships
- 7.6 Transformations part II: Impacts on SLR interpretations: log(y), log(x), & both log(y) & log(x)
- 7.7 Confidence interval for the mean and prediction intervals for a new observation
- 7.8 Chapter summary
- 7.9 Summary of important R code
- 7.10 Practice problems
- 8 Multiple linear regression
- 8.1 Going from SLR to MLR
- 8.2 Validity conditions in MLR
- 8.3 Interpretation of MLR terms
- 8.4 Comparing multiple regression models
- 8.5 General recommendations for MLR interpretations and VIFs
- 8.6 MLR inference: Parameter inferences using the t-distribution
- 8.7 Overall F-test in multiple linear regression
- 8.8 Case study: First year college GPA and SATs
- 8.9 Different intercepts for different groups: MLR with indicator variables
- 8.10 Additive MLR with more than two groups: Headache example
- 8.11 Different slopes and different intercepts
- 8.12 F-tests for MLR models with quantitative and categorical variables and interactions
- 8.13 AICs for model selection
- 8.14 Case study: Forced expiratory volume model selection using AICs
- 8.15 Chapter summary
- 8.16 Summary of important R code
- 8.17 Practice problems
- 9 Case studies
- 9.1 Overview of material covered
- 9.2 The impact of simulated chronic nitrogen deposition on the biomass and N2-fixation activity of two boreal feather moss–cyanobacteria associations
- 9.3 Ants learn to rely on more informative attributes during decision-making
- 9.4 Multi-variate models are essential for understanding vertebrate diversification in deep time
- 9.5 What do didgeridoos really do about sleepiness?
- 9.6 General summary
- References
7.5 Transformations part I: Linearizing relationships
When the influential point, linearity, constant variance and/or normality assumptions are clearly violated, we cannot trust any of the inferences generated by the regression model. The violations occur on gradients from minor to really major problems. As we have seen from the examples in the previous chapters, it has been hard to find data sets that were free of all issues. Furthermore, it may seem hopeless to be able to make successful inferences in some of these situations with the previous tools. There are three potential solutions to violations of the validity conditions:
Consider removing an offending point or two and see if this improves the results, presenting results both with and without those points to describe their impact106,
Try to transform the response, explanatory, or both variables and see if you can force the data set to meet our SLR assumptions after transformation (the focus of this and the next section), or
Consider more advanced statistical models that can account for these issues (the focus of subsequent statistics courses, if you continue on further).
Transformations involve applying a function to
one or both variables.
After applying this transformation, one hopes to have
alleviated whatever issues encouraged its consideration. Linear transformation
functions, of the form \(z_{\text{new}}=a*x+b\), will never help us to fix
assumptions in regression situations; linear transformations change the scaling
of the variables but not their shape or the relationship between two variables.
For example, in the Bozeman Temperature data example, we subtracted 1901 from
the Year variable to have Year2 start at 0 and go up to 113. We could
also apply a linear transformation to change Temperature from being measured in
\(^\circ F\) to \(^\circ C\) using \(^\circ C=[^\circ F - 32] *(5/9)\). The
scatterplots on both the original and transformed scales are provided in
Figure 2.135. All the
coefficients in the regression model and the labels on the axes change, but the
“picture” is still the same. Additionally, all the inferences remain the same –
p-values are unchanged by linear transformations. So linear transformations
can be “fun” but really are only useful if they make the coefficients easier to
interpret.
Here if you like temperature changes in \(^\circ C\) for a 1 year increase, the
slope coefficient is 0.029 and if you like the original change in \(^\circ F\) for
a 1 year increase, the slope coefficient is 0.052. More useful than this is the switch into units of 100 years (so each year increase would just be 0.1 instead of 1), so that the slope is the temperature change over 100 years.
(ref:fig7-11) Scatterplots of Temperature (\(^\circ F\)) versus Year (left) and Temperature (\(^\circ C\)) vs Years since 1901 (right).
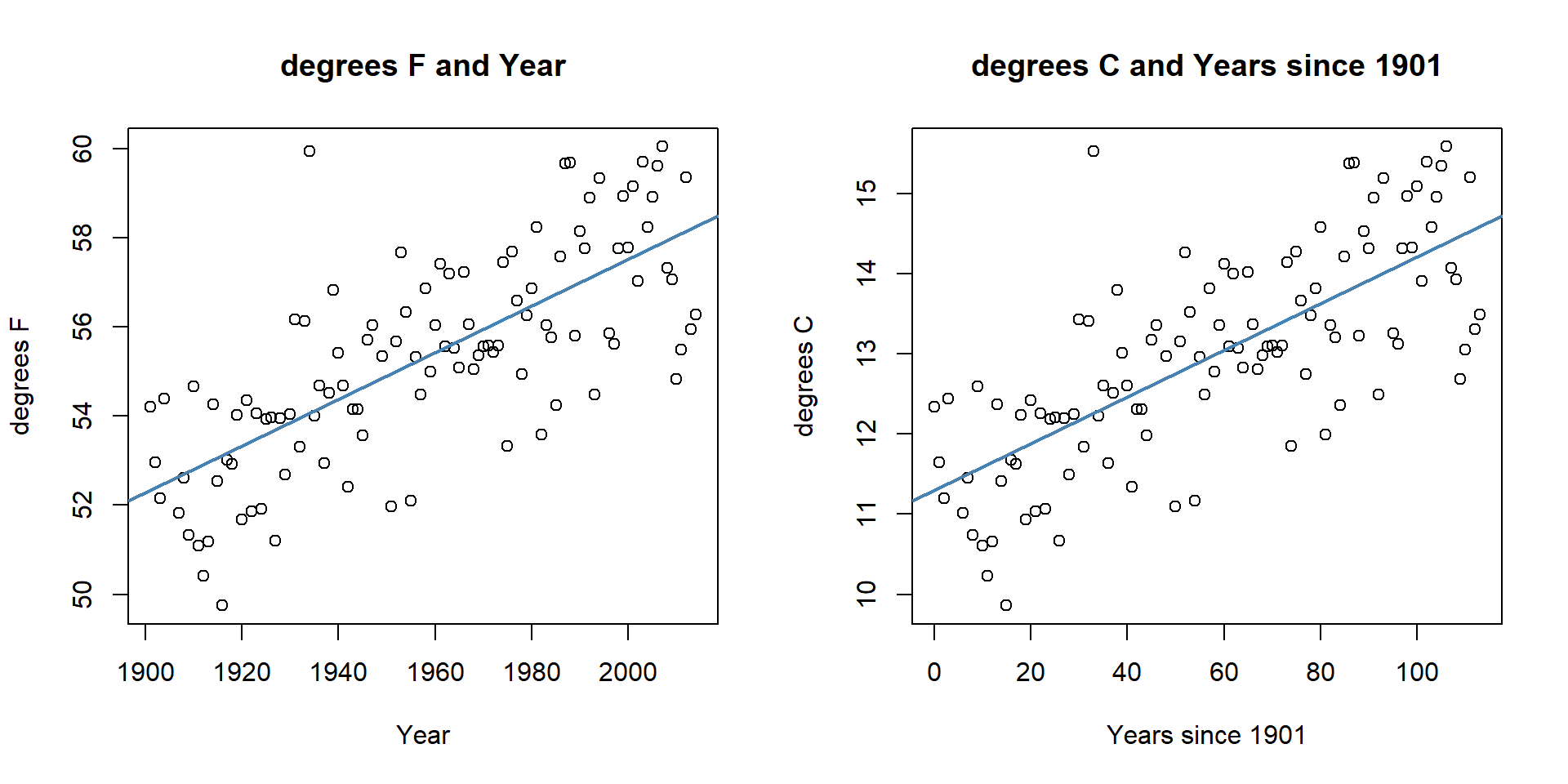
Figure 2.135: (ref:fig7-11)
bozemantemps$meanmaxC <- (bozemantemps$meanmax - 32)*(5/9)
temp3 <- lm(meanmaxC~Year2, data=bozemantemps)##
## Call:
## lm(formula = meanmax ~ Year, data = bozemantemps)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.3779 -0.9300 0.1078 1.1960 5.8698
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -47.35123 9.32184 -5.08 1.61e-06
## Year 0.05244 0.00476 11.02 < 2e-16
##
## Residual standard error: 1.624 on 107 degrees of freedom
## Multiple R-squared: 0.5315, Adjusted R-squared: 0.5271
## F-statistic: 121.4 on 1 and 107 DF, p-value: < 2.2e-16##
## Call:
## lm(formula = meanmaxC ~ Year2, data = bozemantemps)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.8766 -0.5167 0.0599 0.6644 3.2610
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.300703 0.174349 64.82 <2e-16
## Year2 0.029135 0.002644 11.02 <2e-16
##
## Residual standard error: 0.9022 on 107 degrees of freedom
## Multiple R-squared: 0.5315, Adjusted R-squared: 0.5271
## F-statistic: 121.4 on 1 and 107 DF, p-value: < 2.2e-16Nonlinear transformation functions are where we apply something more complicated than this shift and scaling, something like \(y_{\text{new}}=f(y)\), where \(f(\cdot)\) could be a log or power of the original variable \(y\). When we apply these sorts of transformations, interesting things can happen to our linear models and their problems. Some examples of transformations that are at least occasionally used for transforming the response variable are provided in Table 2.12, ranging from taking \(y\) to different powers from \(y^{-2}\) to \(y^2\). Typical transformations used in statistical modeling exist along a gradient of powers of the response variable, defined as \(y^{\lambda}\) with \(\boldsymbol{\lambda}\) being the power of the transformation of the response variable and \(\lambda = 0\) implying a log-transformation. Except for \(\lambda = 1\), the transformations are all nonlinear functions of \(y\).
(ref:fig7-12) Scatterplots of Hectares (a) and log-Hectares (b) vs Temperature.
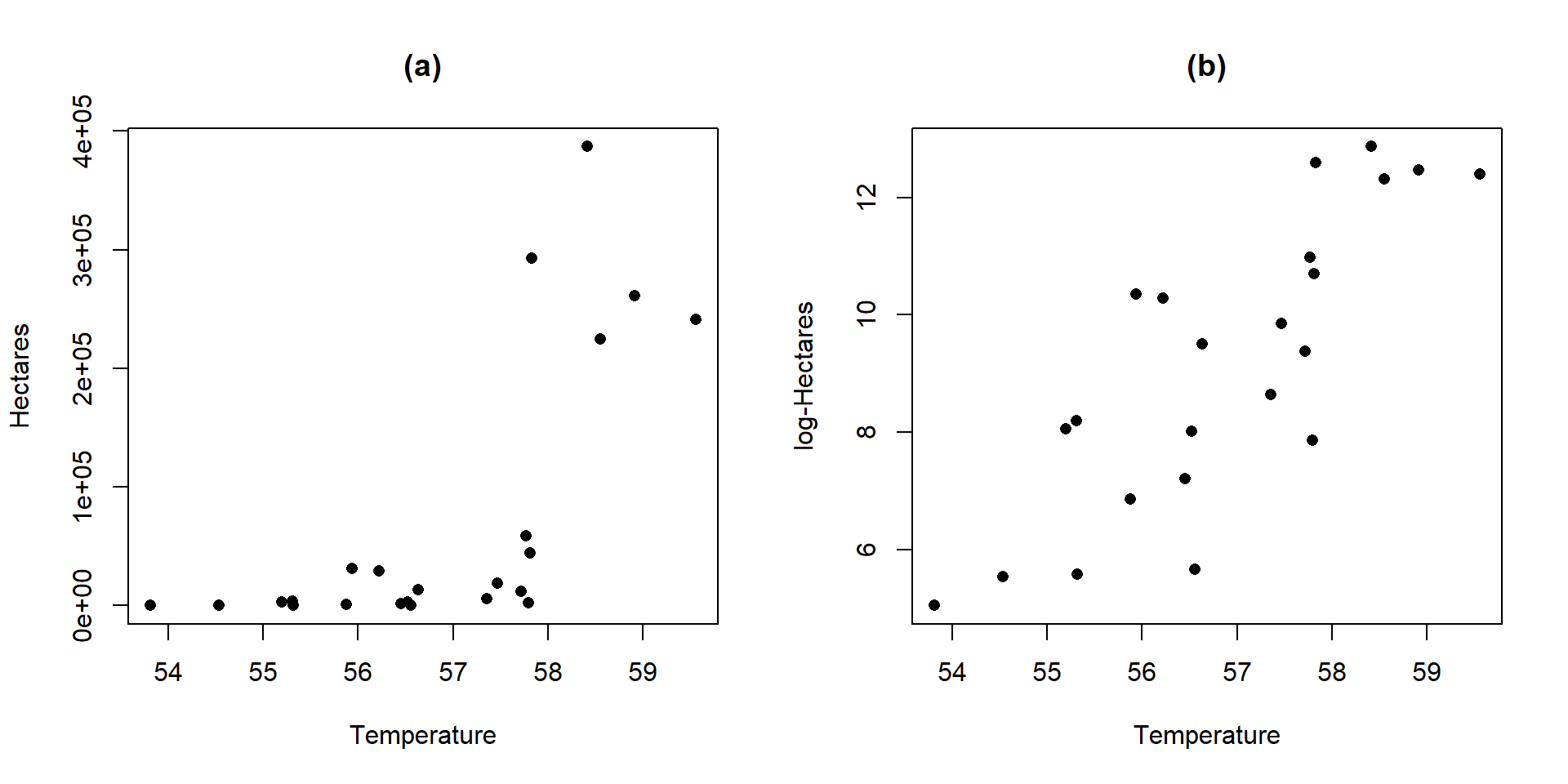
Figure 2.136: (ref:fig7-12)
(ref:tab7-1) Ladder of powers of transformations that are often used in statistical modeling.
| Power | Formula | Usage |
|---|---|---|
| 2 | \(y^2\) | seldom used |
| 1 | \(y^1=y\) | no change |
| \(1/2\) | \(y^{0.5}=\sqrt{y}\) | counts and area responses |
| 0 | \(\log(y)\) natural log of \(y\) | counts, normality, curves, non-constant variance |
| \(-1/2\) | \(y^{-0.5}=1/\sqrt{y}\) | uncommon |
| \(-1\) | \(y^{-1}=1/y\) | for ratios |
| \(-2\) | \(y^{-2}=1/y^2\) | seldom used |
There are even more transformations possible, for example \(y^{0.33}\) is sometimes useful for variables involved in measuring the volume of something. And we can also consider applying any of these transformations to the explanatory variable, and consider using them on both the response and explanatory variables at the same time. The most common application of these ideas is to transform the response variable using the log-transformation, at least as a starting point. In fact, the log-transformation is so commonly used (or maybe overused), that we will just focus on its use. It is so commonplace in some fields that some researchers log-transform their data prior to even plotting it. In other situations, such as when measuring acidity (pH), noise (decibels), or earthquake size (Richter scale), the measurements are already on logarithmic scales.
Actually, we have already analyzed data that benefited from a log-transformation – the log-area burned vs. summer temperature data for Montana. Figure 2.136 compares the relationship between these variables on the original hectares scale and the log-hectares scale.
par(mfrow=c(1,2))
plot(hectares~Temperature, data=mtfires, main="(a)",
ylab="Hectares", pch=16)
plot(loghectares~Temperature, data=mtfires, main="(b)",
ylab="log-Hectares", pch=16)Figure 2.136(a) displays a relationship that would be hard fit using SLR – it has a curve and the variance is increasing with increasing temperatures. With a log-transformation of Hectares, the relationship appears to be relatively linear and have constant variance (in (b)). We considered regression models for this situation previously. This shows at least one situation where a log-transformation of a response variable can linearize a relationship and reduce non-constant variance.
This transformation does not always work to “fix” curvilinear relationships, in fact in some situations it can make the relationship more nonlinear. For example, reconsider the relationship between tree diameter and tree height, which contained some curvature that we could not account for in an SLR. Figure 2.137 shows the original version of the variables and Figure 2.138 shows the same information with the response variable (height) log-transformed.
library(spuRs)
data(ufc)
ufc <- as_tibble(ufc)
scatterplot(height.m~dbh.cm, data=ufc[-168,], smooth=list(spread=F),
main="Tree height vs tree diameter")
scatterplot(log(height.m)~dbh.cm, data=ufc[-168,], smooth=list(spread=F),
main="log-Tree height vs tree diameter")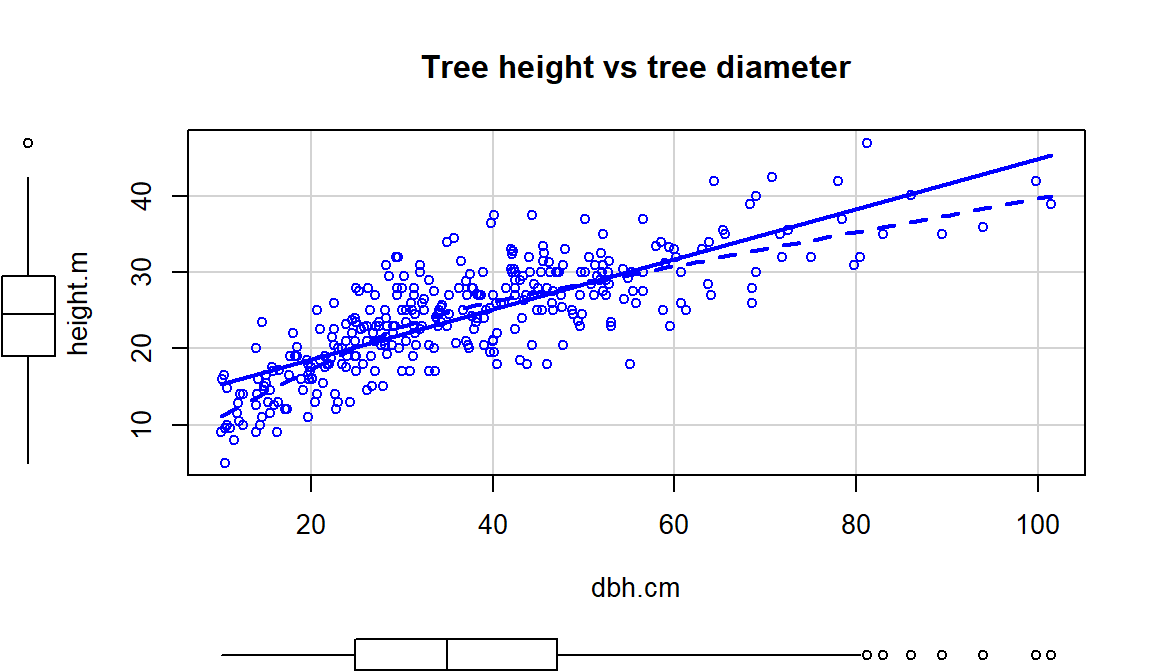
Figure 2.137: Scatterplot of tree height versus tree diameter.
Figure 2.138 with the log-transformed height response seems to show a more nonlinear relationship and may even have more issues with non-constant variance. This example shows that log-transforming the response variable cannot fix all problems, even though I’ve seen some researchers assume it can. It is OK to try a transformation but remember to always plot the results to make sure it actually helped and did not make the situation worse.
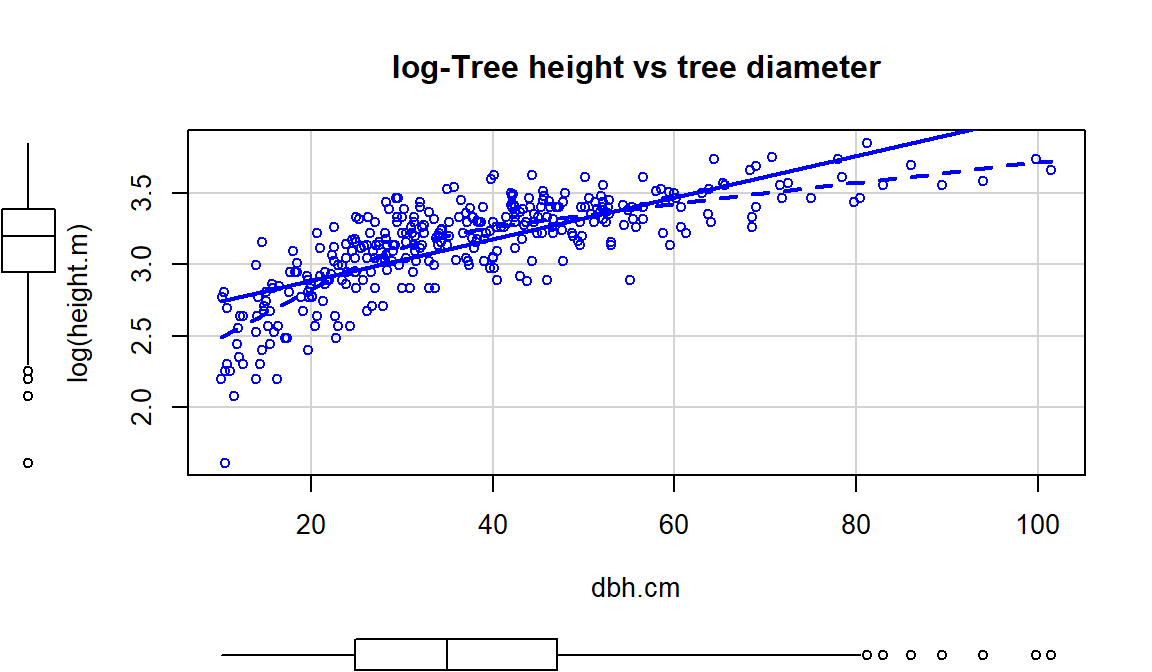
Figure 2.138: Scatterplot of log(tree height) versus tree diameter.
All is not lost in this situation, we can consider two other potential
uses of the log-transformation
and see if they can “fix” the relationship up a bit. One option is to apply the
transformation to the explanatory variable (y~log(x)), displayed in
Figure 2.139. If the distribution of the explanatory
variable is right skewed (see the boxplot on
the x-axis), then consider log-transforming the explanatory variable. This will
often reduce the leverage of those most extreme observations which can be
useful. In this situation, it also seems to have been quite successful at
linearizing the relationship, leaving some minor
non-constant variance, but providing a big improvement from the relationship on
the original scale.
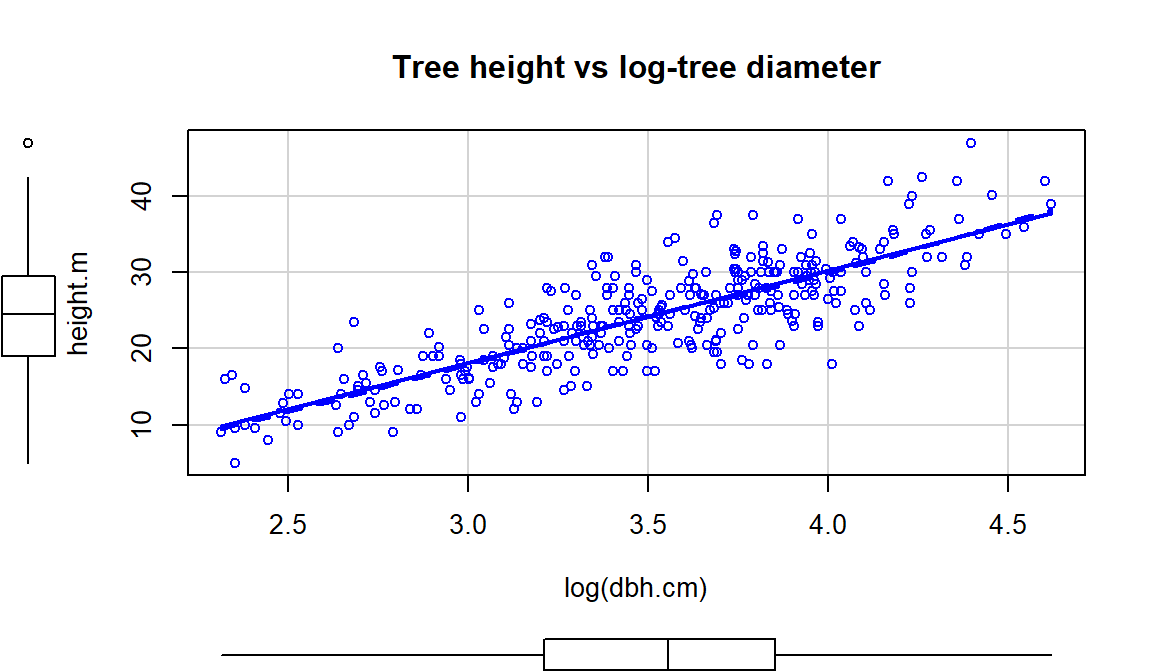
Figure 2.139: Scatterplot of tree height versus log(tree diameter).
The other option, especially when everything else fails, is to apply the
log-transformation to
both the explanatory and response variables (log(y)~log(x)), as
displayed in Figure 2.140. For this example, the
transformation seems to be better than the first two options
(none and only \(\log(y)\)), but demonstrates some decreasing variability with
larger \(x\) and \(y\) values. It has also created a new and different curve in the relationship (see the smoothing (dashed) line start below the SLR line, then go above it, and the finish below it). In the end, we might prefer to fit an SLR model to the
tree height vs log(diameter) versions of the variables
(Figure 2.139).
scatterplot(log(height.m)~log(dbh.cm), data=ufc[-168,], smooth=list(spread=F),
main="log-Tree height vs log-tree diameter")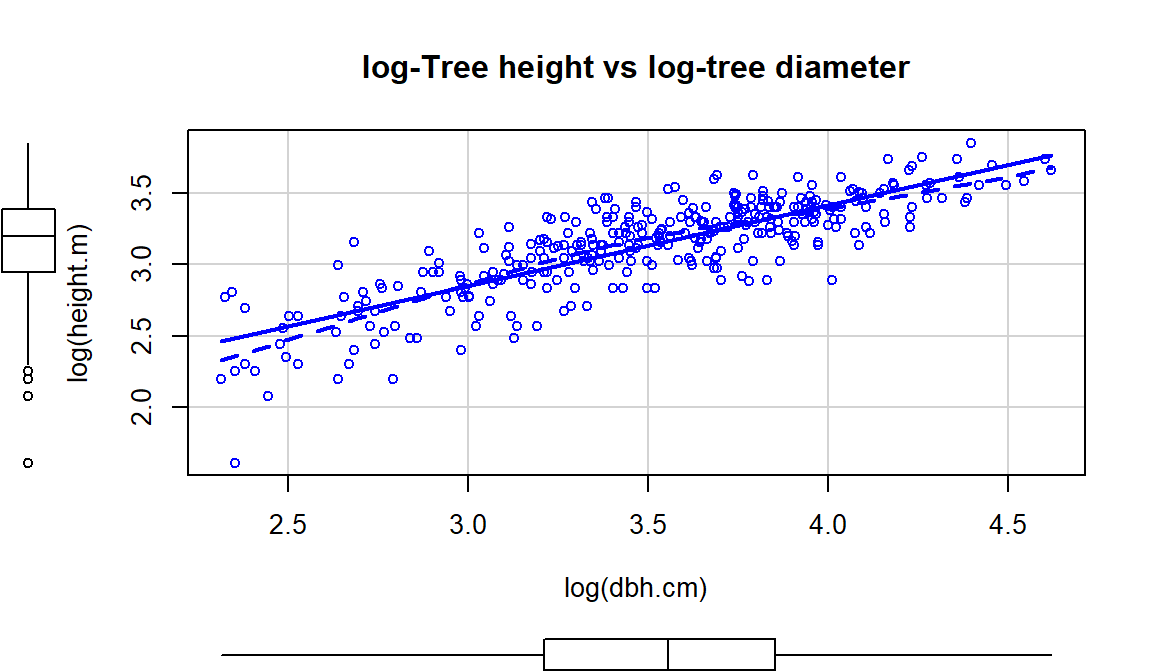
Figure 2.140: Scatterplot of log(tree height) versus log(tree diameter).
Economists also like to use \(\log(y) \sim \log(x)\) transformations. The log-log transformation tends to linearize certain relationships and has specific interpretations in terms of Economics theory. The log-log transformation shows up in many different disciplines as a way of obtaining a linear relationship on the log-log scale, but different fields discuss it differently. The following example shows a situation where transformations of both \(x\) and \(y\) are required and this double transformation seems to be quite successful in what looks like an initially hopeless situation for our linear modeling approach.
Data were collected in 1988 on the rates of infant mortality
(infant deaths per 1,000
live births) and gross domestic product (GDP) per capita (in 1998 US dollars)
from \(n=207\) countries. These data are available from the carData package
(Fox, Weisberg, and Price (2018), Fox (2003)) in a data set called UN.
The four panels in
Figure 2.141 show the original relationship and the impacts of
log-transforming one or both variables.
The only scatterplot that could potentially be modeled using SLR is the lower
right panel (d) that shows the relationship between log(infant mortality)
and log(GDP). In the next section, we will fit models to some of these
relationships and use our diagnostic plots to help us assess “success” of
the transformations.
(ref:fig7-17) Scatterplots of Infant Mortality vs GDP under four different combinations of log-transformations.
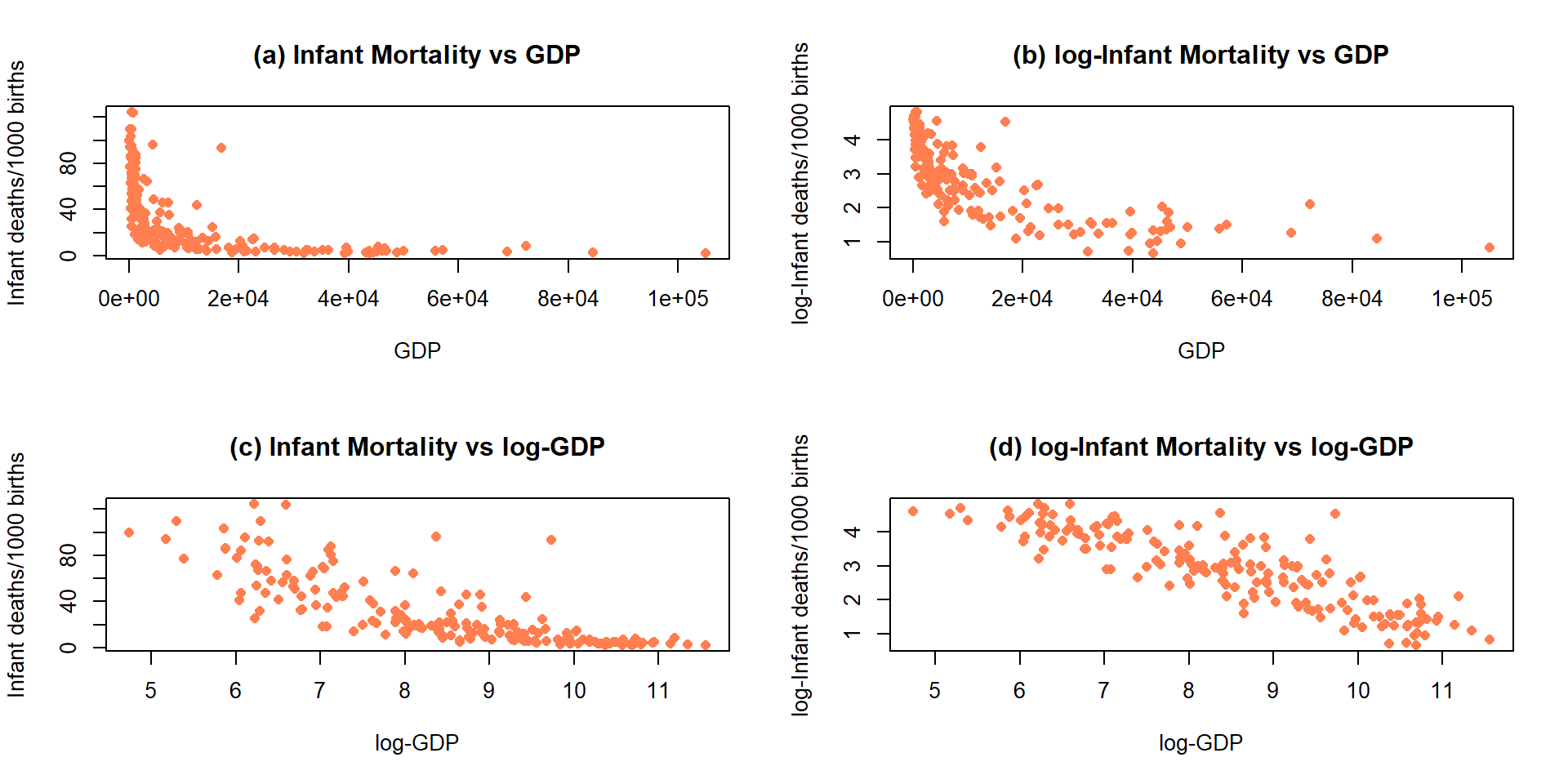
Figure 2.141: (ref:fig7-17)
Almost all nonlinear transformations assume that the variables are strictly
greater than 0. For example, consider what happens when we apply the
log function to 0 or a negative value in R:
## [1] NaN## [1] -InfSo be careful to think about the domain of the transformation function before using transformations. For example, when using the log-transformation make sure that the data values are non-zero and positive or you will get some surprises when you go to fit your regression model to a data set with NaNs (not a number) and/or \(-\infty\text{'s}\) in it. When using fractional powers (square-roots or similar), just having non-negative values are required and so 0 is acceptable.
Sometimes the log-transformations will not be entirely successful. If the relationship is monotonic (strictly positive or strictly negative but not both), then possibly another stop on the ladder of transformations in Table 2.12 might work. If the relationship is not monotonic, then it may be better to consider a more complex regression model that can accommodate the shape in the relationship or to bin the predictor, response, or both into categories so you can use ANOVA or Chi-square methods and avoid at least the linearity assumption.
Finally, remember that log in statistics and especially in R means the
natural log (ln or log base e as you might see it elsewhere). In
these situations, applying the log10 function (which provides log base 10)
to the variables would lead to very similar results, but readers may assume
you used ln if you don’t state that you used \(log_{10}\). The main thing
to remember to do is to be clear when communicating the version you are
using. As an example, I was working with researchers on a study
(Dieser, Greenwood, and Foreman 2010) related to impacts of environmental
stresses on bacterial survival. The response variable was log-transformed
counts and involved smoothed regression lines fit on this scale. I was using
natural logs to fit the models and then shared the fitted values from the
models and my collaborators back-transformed the results assuming that I had
used \(log_{10}\). We quickly resolved our differences once we discovered them but
this serves as a reminder at how important communication is in group projects
– we both said we were working with log-transformations and didn’t know that we
defaulted to different bases.
| Generally, in statistics, it’s safe to assume |
| that everything is log base e unless otherwise specified. |
References
Dieser, Markus, Mark C. Greenwood, and Christine M. Foreman. 2010. “Carotenoid Pigmentation in Antarctic Heterotrophic Bacteria as a Strategy to Withstand Environmental Stresses.” Arctic, Antarctic, and Alpine Research 42(4): 396–405. https://doi.org/10.1657/1938-4246-42.4.396.
Fox, John. 2003. “Effect Displays in R for Generalised Linear Models.” Journal of Statistical Software 8 (15): 1–27. http://www.jstatsoft.org/v08/i15/.
Fox, John, Sanford Weisberg, and Brad Price. 2018. CarData: Companion to Applied Regression Data Sets. https://CRAN.R-project.org/package=carData.
If the removal is of a point that is extreme in \(x\)-values, then it is appropriate to note that the results only apply to the restricted range of x-values that were actually analyzed in the scope of inference discussion. Our results only ever apply to the range of \(x\)-values we had available so this is a relatively minor change.↩